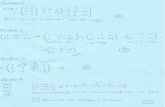Álgebra Linear-Aula Slide

5/21/2018 lgebra Linear-Aula Slide

1/61

E

Prof. Carlos Alexandre Barros de [email protected] 1

. C A @..


2/61

E

,

, : , ,

, , ,


, , , ,

:


3/61

E

) (+ ) + = + (+ )

) + = +

) + =


) E + () =

) (+ ) = + ,

) (+ )= + , ,

) ()= ()

) 1.=


4/61

E

D

E


= (2, 2) 22


5/61

E

= (2, 2) Axioma 1: (u + v) + w = u + (v + w)

( ) wvu

++

=

+

+

=++2221

1211

2221

1211

2221

1211

wwvuvu

ww

ww

vv

vv

uu

uu


( ) ( )

( ) ( )

( ) ( )

( ) ( )

( ) ( )

( ) ( )

( ) ( )

( )wvu ++=

+

+

=

=

++

+++

=

=

++++

++++=

++++

++++=

=+ ++=

2221

1211

2221

1211

2221

1211

22222121

12121111

2221

1211

222222212121

121212111111

222222212121

121212111111

222122222121

ww

ww

vv

vv

uu

uu

wvwv

wvwv

uu

uu

wvuwvu

wvuwvu

wvuwvu

wvuwvu

wwvuvu


6/61

E

= (2, 2)

Operao vetorial genrica

Axioma 2: u + v = v + u


11 12 11 12 11 12 11 12

21 22 21 22 21 22 21 22

u u v v v v u u

u u v v v v u u

+ = + = + = +

u v v u

Interpretao concreta


7/61

E

= (2, 2)

Axioma 3: Existe um elemento 0 em V, chamado um vetor nulopara V, tal que u + 0 = u para todo u em V.

0

Ento.00

Se a


u0uu =

=

+

=+

2221

1211

2221

1211

00

00,

00

uu

uu

uu

uuV


8/61

E

= (2, 2)

Axioma 4: Para todo u em V, h um objetou em V, chamado umoposto ou negativo ou simtrico de u, tal que u + (-u) = 0

u

Ento,.Seja 1211 uu


( )

0

uuu

=

=

=

++++

=

+

=+

0000

)()()()(

,

22222121

12121111

22222121

12121111

2221

1211

2221

1211

2221

uuuu

uuuu

uuuu

uuuu

uu

uu

uu

uuV


9/61

E

= (2, 2)

Axioma 5: k (u + v) = k u + k v

( )vuvv

vv

uu

uukk =

+

=+

2221

1211

2221

1211


( ) ( )( ) ( )

vu kkvkvk

vkvk

ukuk

ukuk

vkukvkuk

vkukvkuk

vukvuk

vukvuk

vuvu

vuvuk

+=

+

=

++

++

=

++

++=

++

++=

2221

1211

2221

1211

22222121

12121111

22222121

12121111

22222121

12121111


10/61

E

= (2, 2)

Axioma 6: (k + l ) u = k u + l u

( ) ( )uuu

lklk =

+=+ 1211


( ) ( )

( ) ( )

uu lkulul

ulul

ukuk

ukuk

ulukuluk

ulukuluk

ulkulk

ulkulk

+=

+

=

=

++

++=

++

++=

2221

1211

2221

1211

22222121

12121111

2221

1211


11/61

E

= (2, 2)

Axioma 7: k(l u) = (k l ) (u)

( )uuu

uulklk =

=

2221

1211


( ) ( )( ) ( )

( ) ( )ulk

uu

uulk

ulkulk

ulkulk

ulkulk

ulkulk

ulul

ululk

=

=

=

=

=

2221

1211

2221

1211

2221

1211

2221

1211


12/61

E

= (2, 2)

Axioma 8: 1u = u

uu =

=

=

=

2221

1211

2221

1211

2221

1211

11

1111

uu

uu

uu

uu

uu

uu



13/61

E

:

= ( ) = ( )

= 2 :


+

= ( ) = ( )

, 8 , :

= ( ) = ( )


14/61

D , , ,

: ) , , + ) , ,



15/61

1) A (

)

I


,

A, ()

() ,


16/61

2)

( ()

= 0)


3) , , ( ):


17/61

= 3 ,

Observe que, se Wno passasse


W ,

Os nicos subespaos de R3 so aorigem, as retas e planos que passam

pela origem e o prprio R3


18/61

= 5 = (0,2,3,4,5);

I , 5

() ():


():= (0, 2, 3, 4, 5), = (0, 2, 3, 4, 5)

E: +=(0, 2+2, 3+3, 4+4, 5+5)

() = (0, 2, 3, 4, 5)

, 5.


19/61

Teorema: Interseo de subespaos Dados W1 e W2subespaos de um espao vetorial

V, a interseo W1 W2ainda um subespao deV

Observe que W1 W2nunca vazio j que eles sempre


con m, pe o menos, o ve or nu o

Exemplo 1: V = R3, W1 W2 a reta deinterseo dos planos W1 e W2

W1

W2


20/61

Embora a interseo gere um subespaovetorial, isso necessariamente no acontece

com a unio Teorema: Soma de subespaos

Se am W e W subes a os de um es a o vetorial


V. Ento o conjunto W1 + W2= {vV; v=w1 + w2, w1W1, w2W2}

subespao de V

Exemplo 1: Se W1 e W2so duas retas, W =W1+W2 o plano que contm as retas


21/61

Quando W1 W2 = {0}, ento W1 + W2

chamado soma diretade W1 com W2,



22/61

C

Sejam Vum espao vetorial real, v1, v2, ..., vnVe a1, a2, ...,an nmeros reais

Ento o vetor v = a1v1 + a2v2 + .... anvn


combinao linearde v1, v2, ..., vn Uma vez fixados vetores v1, v2, ..., vn em V, o

conjunto Wde todos os vetores de Vque so

combinao linear desse um subespao vetorial W chamado de subespao gerado por v1, v2, ..., vn W = [v1, v2, ..., vn]


23/61

C

Exemplo 1:V= R2, v1 = (1, 0), v2 = (0, 1) Logo, V= [v1, v2], pois dados v = (x, y)V, temos (x,

y) = x(1, 0) + y(0, 1) Ou seja, v = x.v1 + y.v2 Exemplo 2:


1 00 0

v1 = 0 10 0v2 =

Ento [v1, v2] = : a, b Ra b0 0


24/61

D I

Definio: Sejam Vum espao vetorial e v1, v2,..., vnV. Dizemos que o conjunto {v1,v2, ...,vn}

linearmente independente(LI), ou que o vetoresv1, v2, ..., vn so LI se a equao: a1v1 + a2v2 + ... + anvn = 0


implica que a1 = a2 = .... = an = 0 {v1,v2, ...,vn} LD se, e somente se, um destes

vetores for combinao linear dos outros.

Se algum ai 0, dizemos que {v1,v2, ...,vn} linearmente dependente(LD) ou que os vetoresv1,v2, ...,vn so LD


25/61

D I

Exemplo 1: V= R2, e1 = (1, 0) e e2 = (0, 1) e1 e e2 so LI, pois

a1.e1 + a2.e2 = 0 a1.(1, 0) + a2.(0, 1) = 0 (a1, a2) = (0, 0)


a1

= e a2

=

Exemplo 2: De modo anlogo, para V=R3, e1= (1, 0, 0), e2 = (0, 1, 0) e e3 = (0, 0, 1) so LI

Exemplo 3: V= R2

{(1, -1), (1, 0), (1, 1)} LD pois: .(1, -1) -1.(1, 0) + .(1, 1) = (0, 0)


26/61

B E

Definio: Um conjunto {v1,v2, ...,vn} de

vetores de Vser uma basede Vse:


n

ii) [v1,v2, ...,vn] V

Esse conjunto gera todos os vetores de V.


27/61

B E

Exemplo 1: V= R2, e1=(1,0) e e2=(0,1) {e1, e2} base de V, conhecida como base

cannica de R2 O conjunto {(1,1),(0,1)} tambm uma base de

= 2


De fato, se (0,0) = a(1,1) + b(0,1) = (a, a + b), ento

a = b = 0 Assim, {(1, 1), (0, 1)} LI

Ainda [(1, 1), (0, 1)] = Vpois dado v = (x, y) V,temos: (x, y) = x(1, 1) + (y x)(0, 1)Ou seja, todo vetor de R2 uma combinao linear

dos vetores (1,1) e (0,1)


28/61

B E

Exemplo 2: {(0,1), (0,2)} no base de R2,pois um conjunto LD

Se (0,0) = a(0,1) + b(0,2), ento a = -2b e ae bnoso zero necessariamente

Exemplo 3: {(1,0,0), (0,1,0), (0,0,1)} uma


base de R3

Base cannica de R3

i) {e1, e2, e3} LI

ii) (x, y, z) = x.e1 + y.e2 + z.e3 Exemplo 4: {(1,0,0), (0,1,0)} no base de R3

LI mas no gera todo R3


29/61

B E

Teorema: Sejam v1,v2, ...,vn vetores no nulosque geram um espao vetorial V. Ento dentre

esses vetores podemos extrair uma base de V. Isso independe de v1,v2, ...,vn serem LD ou LI


Teorema: Seja um espao vetorial Vgeradopor um conjunto finito de vetores v1,v2,...,vn. Ento, qualquer conjunto com mais de n

vetores necessariamente LD (e, portanto,qualquer conjunto LI tem no mximo nvetores)


30/61

B E

Corolrio: Qualquer base de um espaovetorial tem sempre o mesmo nmero de

elementos. Este nmero chamado dimensode V, e denotado por dim V Exem lo 1: V = R2: dim V= 2


{(1,0), (0,1)} e {(1,1),(0,1)} so bases de V Exemplo 2: V = R3: dim V= 3 Exemplo 3: V = M(2, 2): dim V= 4

1 00 0

0 10 0

umabase de V

0 01 0

0 00 1


31/61

B E

Teorema: Qualquer conjunto de vetores LI de umespao vetorial Vde dimenso finita pode ser

completado de modo a formar uma base de V Corolrio: Se dim V = n, qualquer conjunto de n

vetores LI formar uma base de V


Teorema: Se Ue Wso subespaos de umespao vetorial Vque tem dimenso finita, entodim U dim V e dim W dim V. Alm disso:

dim(U + W) = dim U+ dim W dim(U W)


32/61

B E

Teorema: Dada uma base = {v1,v2, ...,vn} deV, cada vetor de V escrito de maneira nica

como combinao linear de v1, v2, ...,vn. Definio: Sejam = {v1,v2, ...,vn} base de Ve

v Vonde v = a v +...+ a v . Chamamos


esses nmeros ai de coordenadas de v emrelao base e denotamos por:

[v] =

a1...an


33/61

B E

Exemplo 1: V= R2

= {(1, 0), (0, 1)}

(4, 3) = 4.(1, 0) + 3.(0, 1) Logo:

4

Observe que oscoeficientes sorepresentados


,

3como elementosde uma matrizcoluna.


34/61

B E

Exemplo 2: V= R2

= {(1, 1), (0, 1)}

(4, 3) = x.(1, 1) + y.(0, 1) x=4 e y=-1 Logo:

4


,

-1


35/61

B E

Exemplo 3: Observe que a ordem doselementos de uma base influi na matriz das

coordenadas de um vetor em relao estabase V= R2


1 = {(1, 0), (0, 1)} e 2 = {(0, 1), (1, 0)}

[(4, 3)]1

=4

3

[(4, 3)]2

=3

4


36/61

B E

Exemplo 4: Considere:V= {(x, y, z): x + y z = 0}

W= {(x, y, z): x = y}Determine V+ W

Prof. Carlos Alexandre Barros de [email protected]

V: x + y z = 0

z = x + y Base: (x, y, x + y) = x.(1, 0, 1) + y.(0, 1, 1) Logo: Base = [(1, 0 , 1),(0, 1, 1)]

W: x = y Base: (y, y, z) = y.(1, 1, 0) + z.(0, 0, 1) Logo: Base = [(1, 1, 0), (0, 0, 1)]

36

cont


37/61

B E

Exemplo 4: (cont..)Como:V = [(1, 0, 1), (0, 1, 1)]W= [(1, 1, 0), (0, 0, 1)]


Ento V+ W= [(1,0,1), (0,1,1), (1,1,0), (0,0,1)]Mas espera-se que o resultado esteja no R3,

logo essa base deve ter algum elemento LD

37

cont


38/61

B E

Exemplo 4: (cont..) Vamos escalonar....

1 0 10 1 1

1 0 10 1 1

1 0 10 1 1

v1

v2


cont

0 0 1

- -

0 0 1

0 0 1

1 0 10 1 10 0 10 0 0 ED (3)

v

v4


39/61

B E

Exemplo 4: (cont..)Logo V+ W= [(1,0,1), (0,1,1), (0,0,1)]

Assim, V+ W= R3

dim R3 = dim V+ dim W dim(VW)


VW= ??

39

cont


40/61

B E

Exemplo 4: (cont..)VW= {(x,y,z); x + y z = 0 e x = y}

= {(x,y,z); x = y = z/2}= [(1, 1, 2)]


dim (VW) = 1dim R3 = dim V+ dim W dim(VW)dim R3 = 2 + 2 1 = 3

Como esperado....

40


41/61

B

Sejam ={u1,...,un} e = {w1,...,wn} duas bases

ordenadas de um mesmo espao vetorial V Dado o vetor vV, podemos escrev-lo como:


v = x1u1 + ... + xnun

v = y1w1 + ... + ynwn(1)

41


42/61

B

Como podemos relacionar as coordenadas dev em relao base

[v] =x

1x


com as coordenadas do mesmo vetor v emrelao base

[v] =

y1yn

42


43/61

B

J que {u1,...,un} base de V, podemos escreveros vetores v e w como combinao linear dos uj,

isto : w1 = a11u1 + a21u2 + ...+ an1unw2 = a12u1 + a22u2 + ...+ an2un


......wn = a1nu1 + a2nu2 + ...+ annun

Substituindo (2) em (1):

v=y1w1+...+ynwn=y1(a11u1+...+an1un)+..+yn(a1nu1+...+annun)= u1(a11y1+...+an1yn)+..+un(a1ny1+...+annyn)

43


44/61

B

Mas v = x1u1 + ... + xnun, e como as coordenadasem relao a uma base so nicas temos:

x1 = a11y1 + ... + an1yn.....xn = a1ny1 + ... + annyn

Observe que as linhasviraram colunas!


Ou, em forma matricial

44

x1xn

y1yn

=a11 ... a1n an1 ann


45/61

B

Isso denotado por:

=a

11

... a1n

a a[ I ]


Temos:

45

[v] = [ I ] [v]

[ I ] Matriz de mudana da base para a base

B


46/61

B

Observe que, encontrando , podemos

encontrar as coordenadas de qualquer vetor vem relao base , multiplicando a matriz

[ I ]


pelas coordenadas de v na base

46

B


47/61

B

Exemplo: Sejam ={(2,-1), (3,4)} e ={(1,0),(0,1)}bases de R2:

w1 = (1,0) = a11(2,-1) + a21(3,4) = (2a11+ 3a21, -a11+ 4a21)

[ I ] = ?


11+ 21 = - 11+ 21 =

a11 = 4a21 a21 = 1/11 e a11 = 4/11

w2 = (0,1) = a12(2,-1) + a22(3,4) = (2a12+ 3a22, -a12+ 4a22)

2a12

+3a22

= 0 e -a12

+4a22

= 1

a22 = 2/11 e a12 = -3/11

47

B


48/61

B

Exemplo: (cont.)

Assim:

w1 = (1,0) = (4/11)(2,-1) + (1/11)(3,4) w2 = (0,1) = (-3/11)(2,-1) + (2/11)(3,4)


=4/11 -3/11

1/11 2/11

[ I ]

48

Linhas tornam-secolunas!!!

B


49/61

B

Exemplo: (cont.) Podemos usar essa matriz paraencontrar, por exemplo, [v] para v = (5, -8)

[(5, -8)] = [(5, -8)][ I ]


= =

49

4/11 -3/11

1/11 2/11

5

-8

4

-1

Isto : (5, -8) = 4.(2, -1) + (-1).(3, 4)

A I B


50/61

A I B

Temos [v] = [v]

Um fato importante que e so

[ I ]

[ I ] [ I ]


( )-1 =

50

[ I ] [ I ]

A I B


51/61

A I B

Exemplo:

Do exemplo anterior, vamos calcular a partir

de . Note que fcil de ser

calculada pois a base cannica:

[ I ]

[ I ][ I ]


(2, -1) = 2.(1, 0) + (-1).(0, 1) (3, 4) = 3.(1, 0) + 4.(0, 1)

Assim: =

Ento: = -1 =

51

[ I ]

[ I ]

2 3

-1 42 3-1 4

4/11 -3/11

1/11 2/11


52/61

E

Exerccio 18: Considere o subespao de

R4

gerado pelos vetores v1 = (1,-1,0,0),v2=(0,0,1,1), v3=(-2,2,1,1) e v4=(1,0,0,0)


, - , , , , ,

b) Exiba uma base para [v1,v2,v3,v4]? Qualsua dimenso?

c) [v1,v2,v3,v4] = R4?

52


53/61

E

Exerccio 18:

a) O vetor (2, -3, 2, 2) [v1,v2,v3,v4]? Ou seja, existem a, b, c, d, tal que:

Cont.


, - , , = . ,- , , . , , ,

c.(-2,2,1,1) + d.(1,0,0,0)

53

a 2c + d = 2-a + 2c = -3b + c = 2b + c = 2

1 0 -2 1 2

-1 0 2 0 -30 1 1 0 2


54/61

E

Exerccio 18:

a) O vetor (2, -3, 2, 2) [v1,v2,v3,v4]?Soluo: a = 3, b = 2, c = 0, d = -1

Cont.


, ,

[v1,v2,v3,v4]

54


55/61

E

Exerccio 18:

b) Exiba uma base para [v1,v2,v3,v4]? Qualsua dimenso?

Cont.


-0 0 1 1-2 2 1 11 0 0 0

-0 0 1 10 0 1 10 1 0 0

Com isso, descobrimos que v2 (ou v3) combinaolinear dos outros vetores. Logo, a base formada por[v1,v2,v4] ou [v1, v3, v4].

E


56/61

E

Exerccio 18:

b) Exiba uma base para [v1,v2,v3,v4]? Qualsua dimenso? = =

Cont.


c) [v1,v2,v3,v4] = R4? Como dim Base = 3 e dim R4 = 4, ento

[v1,v2,v3,v4] R4

56

E


57/61

E

Exerccio 19: Considere o subespao de

R3

gerado pelos vetores v1=(1,1,0),v2=(0,-1,1) e v3=(1,1,1).


1, 2, 3 =

57

E


58/61

E

Exerccio 19: Soluo 1:

Existem a, b, c tal que:(x, y, z) = a.(1,1,0) + b.(0,-1,1) + c.(1,1,1)

Cont.


a + c = xa - b = yb + c = z

a = 2x y - zb = x - yc = -x + y + z

Ou seja, h valores para a, b e c quepodem gerar qualquer vetor no R3.

E


59/61

E

Exerccio 19: Soluo 2:

Vamos tentar escalonar:

Cont.

1 1 0 1 0 0


-1 1 1 0 0 1

O que isso significa?

Significa que, com esses vetores e operaeslineares, conseguimos gerar a base cannica.Logo, podemos gerar todo o R3.

E i S id


60/61

Exerccios Sugeridos

2 4 6 7


9 11 15

25 29

A


61/61

A ...


Álgebra Linear-Aula Slide

Documents

Transcript of Álgebra Linear-Aula Slide