Calculadora Colorida e Musical: uma ferramenta para explorar

números racionais.

Maisa Aparecida Siqueira Rodrigues

Orientadora: Lulu Healy

CONSIDERAÇÕES E PROBLEMÁTICA

Muitos alunos no 1º Ano do Ensino Médio apresentam dificuldades em

compreender de forma ampla o conceito de números racionais, mostrando ter uma

compreensão limitada desses números em seus diferentes significados (razão, parte-todo,

quociente, medida e operador).

Observamos em algumas atividades aplicadas em aula, que além das dificuldades

com as operações que envolvem decimais e frações, os alunos apresentam também

dificuldades na interpretação do conceito dos números racionais devido a um forte vinculo

com os conceitos e propriedades dos números naturais ou inteiros. Acreditamos que isso

acontece, pois durante sua escolarização o ensino de matemática está organizado de forma

a privilegiar o trabalho com os números naturais e inteiros sendo que somente a partir da 7ª

série do Ensino Fundamental um ensino que contempla também os números racionais.

Não compreender esse conceito gera outras dificuldades que bloqueiam a

aprendizagem de outras propriedades fundamentais como representar um número decimal

em fração, diferenciar um número racional de um número irracional, identificar uma

dízima periódica, identificar a partir de uma fração se esse número é um decimal exato ou

periódico, etc.

Muitas pesquisas mostram que os problemas relacionados ao ensino e a

aprendizagem dos números racionais são extremamente amplos. Aprender os conceitos e

propriedades desses números continua sendo, ainda, um sério obstáculo no aprendizado

matemático dos alunos. Essa conclusão pode ser verificada, segundo Damico (2007), nas

recentes investigações (Freudenthal, Ohlsson, Bigelow, Davis e Hunting; Kieren) sobre a

construção da idéia de número racional pelos alunos.

Damico (2007) aponta que os resultados da análise pedagógica do Sistema de

Avaliação de Rendimento Escolar do Estado de São Paulo (Saresp, 1998) indicam que

muitos alunos no 1º Ano do Ensino Médio não conseguem resolver situações-problemas

que envolvem operações com números racionais representados na forma fracionária,

sugerindo que isso pode ser resultante da ênfase curricular em procedimentos mecanizados

em detrimento do desenvolvimento da compreensão desses números em seus diferentes

significados.

Os resultados dos últimos Saresp (2005/ 2007) também indicam que os alunos

permanecem com as mesmas dificuldades de identificar e interpretar informações

envolvendo números racionais e seus diferentes significados, como também resolver

situação-problema com esses significados em diferentes contextos, tanto que a nova

proposta do Estado de São Paulo, conhecida como São Paulo Faz Escola (2008) teve como

foco a retomada dessas habilidades na preparação do material para o aluno no 1º Ano do

Ensino Médio (Jornal do Aluno). Essa foi uma edição especial da proposta curricular

trabalhada nos primeiros 42 dias de aula do corrente ano letivo, pois cada série teve um

material preparado com habilidades específicas com a “intenção de reforçar” a formação

escolar do aluno e seu “desempenho” em futuras avaliações.

Em uma revisão preliminar bibliográfica no banco de dados da CAPES sobre esse

tema, encontramos um número significativo de pesquisas relacionadas aos problemas de

aprendizagem do conceito de fração tendo como foco principal à compreensão da

aprendizagem dos alunos no Ensino Fundamental diante de problemas que envolvem

idéias de números racionais em seus diferentes significados. Essas investigações não

enfocam a aprendizagem dos números racionais, em particular os da representação

fracionária e decimal, no Ensino Médio utilizando para isso um recurso tecnológico como

um software.

Além das diferentes dificuldades apresentadas pelos alunos perante problemas que

envolvem o conceito de números racionais, que são confirmadas pelas pesquisas existentes

sobre esse tema, outra questão levantada em nossa pesquisa, é a possibilidade de utilizar

diferentes recursos tecnológicos no ensino da Matemática para tentar amenizar essas

dificuldades e tornar a aprendizagem mais significativa ao aluno e assim possibilitar o seu

envolvimento no processo de ensino-aprendizagem. Segundo os PCN, a utilização de

recursos tecnológicos:

“pode contribuir para que o processo de ensino e aprendizagem de Matemática se torne uma atividade experimental mais rica, sem risco de impedir o desenvolvimento do pensamento, desde que os alunos sejam encorajados a desenvolver seus processos metacognitivos e sua capacidade crítica.” (Brasil 1998, p.45).

O trabalho de Karrer (1999) sobre o uso da calculadora no ensino de logaritmo e o

de Drisostes (2006) sobre design interativo de um micromundo incentivou-nos a

desenvolver uma pesquisa com o objetivo de criar um cenário que propicie o ensino e

aprendizagem de um conteúdo matemático utilizando tecnologia. Esses trabalhos mostram

uma possibilidade de incorporar na prática do ensino de matemática, voltado

tradicionalmente para a oralidade e escrita, diferente maneiras de comunicar, conhecer e

aprender saberes.

Outro fato importante nessa investigação está relacionado com a criação de um

software que atendesse as expectativas dos sujeitos de pesquisa, pois teoricamente, esses

alunos já aprenderam alguns aspectos deste conceito ou pelo menos já trabalharam com os

números racionais no Ensino Fundamental, e para aqueles que ainda não o dominam,

acreditamos que, não se deve simplesmente repetir o mesmo tipo de situação ou método de

ensino, sendo necessário para estes buscar novas maneiras de trabalhar com esse conceito.

Queremos então a partir da compreensão dos alunos sobre números racionais tentar

amenizar as dificuldades que acerca o aprendizado desse saber, dando uma nova

oportunidade para que esses alunos aprender e compreender melhor o conceito desses

números em uma abordagem diferente das que eles já depararam em sua experiência

escolar.

Apoiando nas idéias de Sinclair et al (2006) sobre a Calculadora Colorida vamos

utilizar essa ferramenta nessa pesquisa como uma nova possibilidade de trabalhar o

conceito dos números racionais. A Calculadora Colorida, segundo Sinclair et al (2006), é

um ambiente de aprendizado com características (cor, tamanho e rapidez) que encorajaram

os alunos a explorar os conceitos desses números pela experimentação e investigação.

Nesse estudo, além do trabalho com a representação visual na calculadora, estamos

desenvolvendo também nesse ambiente de aprendizagem, que chamamos de Micromundo,

uma representação sonora dos números racionais atribuindo para cada dígito uma nota

musical, por esse motivo Calculadora Colorida e Musical. A criação da representação

sonora dos números racionais na calculadora colorida está sendo estudada e desenvolvida

junto com o grupo de pesquisa, especialmente com a contribuição de Guilherme Rodrigues

Magalhães e Lulu Healy.

Healy e Sinclair (2007) defendem que tecnologias, como os micromundos, podem

fornecer oportunidades únicas para a emergência de narrativas produtivas, no sentido

destas guiarem os alunos para um entendimento matemático mais profundo e satisfatório

em suas atividades matemáticas. Elas sugerem que essas narrativas são centrais no fazer

sentido do aluno diante um fenômeno matemático e que sua criação específica e sua função

nesse fazer sentido tem sido pouco explorado em pesquisas na Educação Matemática.

As interpretações dos conceitos matemáticos através das narrativas dos alunos,

sugerida por Healy e Sinclair (2007), são fundamentadas pelas idéias de Bruner (1997):

“o poder da narrativa é reconhecido pelo ser humano desde sua infância: o que ele faz, ou deseja fazer, é interpretado não apenas pelo ato em si, mas pelo que é contado a respeito desse ato”.

(Bruner, 1997, apud Sales, 2007; p.1).

Sales (2007) apoiando em Healy e Sinclair (2007) argumenta que “estes ambientes

(micromundos) podem promover oportunidades para produção de narrativas ou estórias

nas atividades matemáticas propostas aos alunos, devido ao seu caráter interativo e

dinâmico”.(p.4), mais especificamente, que as narrativas produzidas que são de interesse

em sua pesquisa, como também em nossa investigação, são aquelas “suscitadas

matematicamente e que indicam como os alunos estão tentando dar sentido para as formas

matemáticas que estudam.” (p.3)

Também acreditamos que esse micromundo Calculadora Colorida e Musical pode

abrir novas possibilidades para a construção de narrativas tornando, assim, a aprendizagem

dos números racionais mais significativa e criativa para o aprendiz, contribuindo, dessa

forma, para um melhor entendimento do papel das narrativas na aprendizagem matemática

Portanto nosso problema de pesquisa se limita em estudar as narrativas produzidas

pelos alunos do 1º Ano do Ensino Médio durante interação com o software Calculadora

Colorida e Musical, porque queremos entender como as estórias, por eles contadas,

contribuem para a construção de novos significados dos números racionais, com o intuito

de descobrir o papel de narrativas na aprendizagem Matemática.

Assim sendo, nossa pesquisa está relacionada com a aprendizagem (para aqueles

que ainda não entenderam) e a resignificação do conceito dos números racionais em alunos

no 1º Ano do Ensino Médio de uma escola Pública, com o objetivo de investigar e analisar

as narrativas, em particular as concepções desses alunos sobre esse conceito que emergem

durante as narrativas elaboradas por eles na interação com o recurso tecnológico a

Calculadora Colorida e Musical.

A CALCULADORA

O uso da calculadora é uma questão bastante polemizada no ensino de matemática.

Uma das discussões sobre o seu uso no ensino é a crença que muitos professores, pais e

alunos tem de que seu uso pode afetar a memória, diminuindo assim a capacidade de

raciocinar. Segundo D’Ambrósio (2003), não existem pesquisas que confirmam esse fato e

atribui a esses temores o excesso de conservadorismo e a falta de visão histórica:

“A história nos ensina que só pode haver progresso científico, tecnológico e social se a sociedade incorporar, no seu cotidiano, todos os meios tecnológicos disponíveis. Assim, depois da invenção da escrita, não se pode justificar que alguém se recuse a ler e escrever... a sociedade se organiza em função da tecnologia disponível. E como se justifica continuar operando com a tecnologia de aritmética de papel, lápis e tabuada?” (D’Ambrósio 2003).

O que D’Ambrósio coloca não é a abolição do lápis e papel no ensino de

matemática, mas sim abrir novas possibilidades nesse ensino incorporando a tecnologia e

permitindo o acesso do aluno, como também, o preparando para se integrar ao mundo

moderno, pois computadores, calculadoras e outros recursos tecnológicos (celulares,

MP3...) estão cada vez mais presentes nas diferentes atividades humanas.

Então visando desenvolver um ambiente computacional focado no domínio dos

números racionais que permite ao aluno a reconstruir e organizar o conceito e propriedades

desses números, trabalhando tanto na representação fracionária como decimal, e também

apresentar uma nova abordagem de ensino para alunos que em algum momento de sua vida

escolar já viram e aprenderam algumas propriedades sobre esses números, mas

apresentavam uma compreensão ainda insatisfatória, Sinclair et al (2006) nesse contexto

desenvolveu a Calculadora Colorida.

A Calculadora Colorida e Musical foi inspirada em Sinclair et al (2006) e além de

fornecer resultados numéricos em uma tabela colorida, agora, também fornece esses

resultados com notas musicais, assim temos uma representação tanto sonora como visual

dos números racionais.

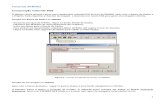
Seu procedimento de uso não se difere muito de uma calculadora comum. Na tela

do computador esta calculadora apresenta simultaneamente uma representação numérica,

visual e sonora para um número decimal, pois cada dígito corresponde a uma cor (visual) e

uma nota musical (sonora), como na figura 1.

Na interface da calculadora (fig. 1) existe um quadro ou tabela em branco que pode

ser pintando quando se realiza uma operação, em especial a divisão, obtendo um número

decimal. Para obtermos o som atrelado ao número racional basta clicar sobre a clave de sol

(fig. 1). Vale salientar que os quatro botões acima dessa clave permitem mudar o tipo de

instrumento, o tempo das notas, o tom e a diferença de tempo entre as notas.

Essa calculadora opera em uma precisão máxima de 500 dígitos decimais, isto é

possível pela troca do tamanho ou dimensão da tabela colorida para valores entre 1 e 50.

Exemplificando, ao realizarmos a operação 1/7 obtém-se o seguinte resultado:

0.14285714285714285714285714285714285714285714285714285714285...

Além da representação decimal apresentada na interface da calculadora, existe uma

tabela ou quadro colorido que representa cada dígito após a vírgula, e a dimensão da tabela

escolhida neste exemplo é 10 (fig. 2). Ao clicar na clave de sol temos o respectivo som

desse número, assim cada resultado é representado simultaneamente por uma seqüência

decimal, uma tabela colorida e um som.

Figura1. - A interface da Calculadora Colorida e Musical.

Figura 2. - A Calculadora Colorida mostra 1/7.

Para explorar as diferentes representações do número 1/7 na tabela colorida, basta

mudar a “extensão da tabela” para obter novas dimensões. Este botão não aparece com o

nome como indica a mostra figura 2, o objetivo é permitir que o aluno descubra através da

interação com a calculadora essas diferentes representações.

Portanto podemos obter diferentes representações coloridas alterando a “extensão

da tabela”, ou seja, o mesmo resultado em diferentes modelos de tabela em diferentes

padrões de cores como podemos observar na figura 3 e figura 4.

Figura 3. - Representação de 1/7 na Calculadora Colorida usando uma tabela de extensão 18.

Extensão da Tabela

Figura 4. Representação de 1/7 na Calculadora Colorida usando uma tabela de extensão 17.

A tabela de extensão 18 (fig. 3) produz um padrão de cor que de acordo com

Sinclair et al (2006) chamamos de listras. Já a tabela de extensão 17 (fig. 4) produz um

padrão que chamamos de diagonais, no caso, à esquerda, pois essas podem aparecer à

direita. No caso em que a tabela colorida aparece com duas cores diferentes alternadas

chamamos esse padrão de tabuleiro, como mostra a figura 4.

Figura 4. - Representação de 1/99 na Calculadora Colorida tem um padrão de tabuleiro.

Vale lembrar que só os dígitos depois do ponto decimal são representados na tabela

colorida e tocados. A operação divisão será o foco do nosso trabalho, pois esta operação

produz a maior parte dos resultados interressantes, particularmente quando o quociente é

um número racional que tem um padrão infinito, ou seja, os quocientes que são dizimas

periódicas.

As quatro características da Calculadora - cor, tamanho, som e rapidez – não são

encontradas em calculadoras portáteis nem por meio da utilização de papel e lápis.

Segundo Sinclair et al (2006) o tamanho da tabela fornece uma repetição de dígitos que

pode ajudar os alunos a perceberam mais facilmente o período do número racional e

criarem uma percepção de infinito.

Com relação à rapidez, Sinclair et al (2006) aponta a habilidade da calculadora

mostrar rapidamente a expansão decimal da fração em contraste com outros ambientes,

como papel e lápis, onde o processo de conversão da fração para o decimal tende a ser

longa, tediosa e propensa para erro. Esta característica leva o aluno a trabalhar com os

resultados da conversão e a tratar estes resultados como objeto ao invés do processo.

A cor facilita a identificação do padrão numérico, pois apresenta diferentes modelos

de representações visuais do mesmo número racional quando manipulamos o tamanho da

grade revelando assim a periodicidade desse número. De acordo com Sinclair et al (2006),

esses modelos são reconhecíveis e atrativos ( listras, diagonais e tabuleiro) e isto pode se

tornar objetos motivacionais. Em nossa investigação, verificamos que o som possui essas

propriedades independentemente da representação visual, conseguindo identificar a

quantidade de dígitos no período da dizima.

Essas características da calculadora permitem encorajar e apoiar a experimentação,

diferente do que ocorre em outros ambientes de aprendizado envolvendo números

racionais, possibilitando uma investigação entre a relação do denominador da fração e o

período da expansão decimal de tal forma que o aluno pela exploração descubra as

propriedades matemáticas existentes.

NARRATIVAS

Das contribuições de Bruner (1997), procuramos fundamentação nas suas idéias

sobre as interpretações dos conceitos matemáticos através das narrativas dos alunos. Ele

sugere que:

“... a narrativa é um modo de pensamento. [...] uma estrutura para organizar nosso conhecimento.” (Bruner, 1997, apud Healy e Sinclair, 2007; p.2).

Segundo Healy e Sinclair (2007), Bruner defende que pelas narrativas, nos

organizamos e formamos nossas experiências no mundo, por isso contamos histórias,

pedimos desculpas e impomos tramas para dar um significado a esse mundo que vivemos.

Para Healy e Sinclair (2007) e Bruner (1997) as narrativas também surgem em nossas

experiências matemáticas.

Para Bruner, narrativas é um dos dois estilos fundamentais do pensamento que

torna possível aos seres humanos fazer suas relações com o mundo: o modo paradigmático

e o modo narrativo.

O modo “paradigmático” ou lógico/classificatório é uma forma explícita de

argumentação sobre o mundo em fatos que refletem o modo formal de pensar (concepções

atemporais e abstratas) usado para se comunicar matematicamente, enquanto que o modo

narrativo está relacionado com as particularidades da experiência e em localizar essa

experiência no tempo e no espaço.

Para identificar mais precisamente o modo narrativo nas histórias contadas pelos

alunos que surgem quando estão tentando dar sentido às experiências matemáticas,

podemos definir quatro características que foram delineadas por Bruner:

• Ter uma seqüência inerente: composta por uma seqüência de eventos que podemos

ver continuidade (isso acontece e então aquilo acontece), comandos são ordenados

e então uma série de eventos casuais com sentido ocorrem, relação temporal.

• Podem ser sobre eventos reais ou imaginários: permite que o mundo imaginário e o

mundo real co-existam, mesmo que temporariamente, essa inter-relação entre o real

e imaginário pode ser vista no desenvolvimento de uma nova matemática, que

começa em um mundo imaginário e migra para o mundo real.

• Forjam conexões entre o excepcional e o ordinário: explicar pela narrativa um

evento extraordinário (o que foge do habitual- complexo) em termos mais

ordinários (habitual familiar- simples)

• Ter algum tipo de qualidade dramática: narrativas que são contadas por pessoas

tentando criar sentido matemático e engajadas no pensamento matemático,

caracterizada pelos antropomorfismos e objetos matemáticos ou inaminados.

Usando a perspectiva de Bruner (1997) como base, narrativa é como um modo de

pensamento que busca dar uma interpretação particular ao conhecimento matemático, um

significado. É baseado nessas idéias que buscaremos analisar as narrativas produzidas

pelos alunos na interação com a Calculadora Colorida e Musical tentando identificar no

modo narrativo características de significação do conceito dos números racionais.

MICROMUNDO

Em relação aos trabalhos de Papert (apud Drisostes, 2006), estamos nos

concentrado até agora na sua visão sobre o construcionismo e nas suas concepções do

conceito de micromundo.

As idéias construcionistas de Papert tiveram como influência as idéias de Piaget

sobre o fato de que o indivíduo constrói o conhecimento a partir de sua ação sobre o objeto

e também aos fatores que influenciam a formação (ou construção) do conhecimento, ou

seja, o conhecimento simplesmente não pode ser transmitido ou transferido.

Os sistemas computacionais para o uso em educação que surgiram das idéias

construcionistas de Papert, eram sistemas que:

“... caracterizavam-se pela busca da liberdade de iniciativa do aprendiz e pelo seu controle do ambiente computacional, neles o aprendizado era entendido como construção pessoal do conhecimento.” (Drisostes, 2006, p.14).

É essa mesma idéia que fundamenta uma abordagem construcionista para

aprendizagem da Matemática em um ambiente computacional, na qual o computador não é

o detentor do conhecimento, mas uma ferramenta que permite ao aluno desenvolver o

pensamento criativo levando-o através do desafio, do conflito e da descoberta a busca de

novas informações e assim construir seu próprio conhecimento.

Nossa pesquisa envolve o design e o uso de micromundo baseada na concepção de

Papert de que “os objetos computacionais devem incorporar uma matemática não apenas

formal, mas também relacionada com o indivíduo permitindo uma abordagem que faz

sentido em matemática e significativa para o aprendiz.”

Também inspirada pela visão de Papert, Healy e Sinclair (2007), define o

micromundo como ambientes computacionais compostos por modelos de um domínio do

conhecimento matemático e por um sistema formal com manifestações fenomenológicas

(físicos, gráfico e ou auditivo) que mostram ações formais desses objetos.

O micromundo, segundo Hoyles e Noss (apud Salles 2007), permite uma forma de

interação entre o aluno e o software, influenciado pela situação didática nas quais essas

interações ocorrem. Uma das características desse ambiente computacional é o fato das

trajetórias de aprendizagem ser controlada pelos aprendizes e não pelo computador, e no

micromundo o aprendiz pode construir sobre o modelo dado obtendo ferramentas mais

complexas a partir de combinações das ferramentas iniciais.

Segundo Healy e Sinclair (2007), em suas pesquisas com tecnologias, as

características da narrativa foram observadas e identificadas nas interações dos aprendizes

com diferentes micromundos computacionais. Elas acreditam que essas tecnologias podem

fornecer oportunidades únicas para narrativas produtivas nas atividades matemáticas dos

aprendizes, pois apresentam três recursos que incentivam a sua criação: movimentos

dinâmicos na tela, tempo no sentido da agilidade dos programas em obter respostas rápidas

e ação.

A Calculadora Colorida é um tipo de micromundo, pois possui uma característica

dinâmica e interativa entre o aprendiz e o conhecimento, incentivando uma exploração que

permite uma melhor compreensão do conceito dos números racionais transitando

simultaneamente entre a representação fracionária e decimal desses números, sendo esse

aprendizado ainda mais significativo se nessa interação surgir narrativas.

METODOLOGIA

A metodologia que estamos utilizando é baseada em Design Research na qual,

segundo Drisostes (2006), o desenvolvimento da pesquisa ocorre através de ciclos

contínuos de design (construção, organização, elaboração), de interação, de análise e de

redesign.

Assim nossa pesquisa está delineada em ciclos contínuos entre a criação da

calculadora como também na elaboração das atividades e na investigação e análise das

interações dos aprendizes com a calculadora.

A criação e o desenvolvimento da calculadora e a elaboração das atividades, é um

processo iterativo, na qual criamos versões da calculadora e atividades a serem testadas em

projetos pilotos para modificar o que não ficou claro ou que está confuso, tanto na

calculadora como nas atividades, colhendo novas sugestões para complementar a criação

desse micromundo.

A investigação e análise das interações dos aprendizes com a calculadora

acontecem num primeiro momento em um projeto piloto para depois num segundo

momento partimos para a pesquisa. Esses momentos envolvem entrevistas de formato

baseadas nas tarefas do micromundo, abrangendo o conteúdo matemático sobre números

racionais que serão gravadas em áudio e vídeo para a análise das expressões dos alunos,

incluindo as anotações registradas em fichas e na tela do computador que pode ser

capturada.

Portanto a análise visará à identificação dos conhecimentos e significados que o

aluno possui em relação aos números racionais, detectando, através das suas falas e dos

seus gestos, possíveis narrativas para os fenômenos matemáticos observados.

ATIVIDADES / RESULTADOS

Vamos apresentar algumas atividades aplicadas e respectivos resultados que foram

relevantes nessa 1ª fase da pesquisa, na qual foi desenvolvido o projeto piloto com a

principal finalidade de testar as atividades e, também a calculadora para possíveis

modificações.

Esse projeto piloto foi aplicado em outubro de 2007, sendo sujeito de pesquisa dois

alunos que estavam cursando o 3º Ano do Ensino Médio de uma escola pública da cidade

de São Paulo que vamos chamar de Antonio e Jéssica.

Apesar de nossa pesquisa estar direcionada para alunos do 1º ano do Ensino Médio,

escolhemos esses sujeitos, pelo fato de estarem terminando um ciclo de sua escolaridade e

por que queríamos além de verificar a compreensão desses alunos através de sua

experiência escolar sobre os números racionais, também queríamos dar uma nova

oportunidade a esses alunos para compreenderem melhor esse conceito através de uma

nova abordagem, permitindo assim uma experiência positiva da Matemática antes saírem

da escola.

No primeiro encontro ocorreram dois momentos, uma entrevista e depois a

apresentação da calculadora. Essa entrevista teve como objetivo fazer uma discussão sobre

os números racionais para situar os alunos no assunto e investigar seu conhecimento sobre

esses números.

Essa entrevista foi realizada em dupla e teve como roteiro as seguintes perguntas:

_Você já deve ter aprendido em algum momento de seus estudos sobre os números

racionais. O que você sabe sobre esses números?

_Escreva alguns números que você sabe que é um número racional.

_Explique por que você sabe que esses números são racionais?

Nas respostas dos alunos podemos identificar certa insegurança sobre o conceito

dos números racionais (especialmente Antonio) e uma tendência a privilegiar os números

inteiros, apresentando uma compreensão superficial sobre esse conceito.

Para Jéssica os números racionais é um conjunto de números que inclui os números

naturais, números inteiros e números primos, considera ainda nesse conjunto qualquer

fração e algumas dízimas periódicas, restringindo os números com raízes, segundo ela, um

número com raíz é irracional. Ela possui um amplo entendimento do conceito de número

racional que se aproxima do conceito matemático desse número, mas se limita quando diz,

com muita insegurança, que os irracionais são raízes, podendo então dizer que √4 é um

número irracional.

Quando Jéssica escreve alguns números racionais coloca vários números inteiros e

apenas um número decimal exato, uma dízima periódica (0, 555...) e uma fração (fig. 5.),

mesmo sabendo que esses números também fazem parte desse conjunto. Ela tenta

relacionar as dízimas periódicas com uma representação fracionária lembrando que “nas

dízimas periódicas se você fizer aquela continha do nove com o zero vai virar fração”,

buscando explicar o algoritmo para encontrar a fração geratriz.

Figura 5.

Já na compreensão de Antonio todos os números são racionais, “para mim, acho

que são todos os números, todos os números”, tanto que reafirma essa condição e quando

exemplifica esses números, fica limitado em escrever números interios e números decimais

exatos (fig. 6.), o que contradiz sua fala por não dar exemplos de números fracionários,

dízimas periódicas, números irracionais e outros, deixando a impressão de que seu

conhecimento sobre números se limita aos de uso cotidiano.

Figura 6.

Quando pedimos para Antonio explicar porque os números que escreveu são

racionais, apontou para os números 1, -6, 8, 20, 50 e 100 dizendo que são inteiros, mas

demonstrou muita insegurança nessa afirmação principalmente quando disse “assim acho

eu” olhando com dúvida para o pesquisador na busca de uma confirmação para o que

estava dizendo. Com relação aos números decimais exatos não consegue explicar “e os

outros, há, eu não consigo explicar”.

Antonio não relaciona esses números com uma possível representação fracionária e

nem levanta a hipótese de dízimas periódica como Jéssica, como podemos observar, sua

compreensão se limita a números inteiros e decimais exatos.

Após entrevista apresentamos a Calculadora Colorida e Musical explorando suas

funções, nesse momento mostramos as operações fundamentais e os diferentes aspectos de

representações (numérica, sonora e visual) que essa Calculadora oferece. Para permitir essa

exploração e a interação do aluno com a calculadora elaboramos uma atividade que foi

realizada em dupla proporcionando o diálogo.

Nosso objetivo nessa atividade, também foi familiarizar e instrumentar o aluno com

a calculadora e observar o seu comportamento, suas impressões, nesse primeiro contato,

deixando-o interagir com as diferentes funções como o tamanho da tabela, instrumentos,

tempo das notas, tom, diferença de tempo entre as notas, música e outras.

A primeira tarefa da atividade proposta para a dupla foi obter as diferentes

representações dos números racionais pela conversão da fração para o decimal, dada pela

seguinte seqüência: 1/1, ½, 1/3, 1/4, 1/5,..., 1/11. Essa atividade, aparentemente simples

possibilitou que os alunos experimentassem as diferentes representações, tanto numérica,

visual e sonora dos números inteiros, decimais exatos e das dízimas periódicas.

Para cada número dessa seqüência os alunos expressaram diferentes reações perante

a representação dada pela calculadora para esse número em sua expansão decimal. Os

números inteiros e aqueles cuja representação decimal é exata (1/1, 1/2, ¼, 1/5, 1/8 e 1/10)

não foram tão interessantes e fascinantes para os alunos como as dízimas periódicas (1/3,

1/6, 1/7, 1/9, 1/11), contrário do que acontece em sala de aula, em que as dízimas não são

nem um pouco atraentes e provocam uma sensação de temor no aluno, pois acreditam ser

mais difícil de compreender.

Primeiro realizamos na calculadora a operação 1/3 para que os alunos observassem

o que estava acontecendo na interface e ouvisse o som tocado, Jéssica logo perguntou:

“por que pintou... por que é infinito” mostrando assim uma percepção de infinito mesmo a

tela sendo limitada. Eles identificaram que o número obtido era uma dízima periódica e

Antonio associou que a cor estava correspondendo a um dígito depois da vírgula “cada

três desse (apontando na tela o dígito depois da vírgula) representa um quadradinho...

azul”. Com relação ao som eles perceberam que sempre toca a mesma nota e que essa nota

corresponde ao dígito depois da vírgula “fica sempre o mesmo som... tutu tu” diz Jéssica,

tanto que Antonio associa esse som ao de um helicóptero.

Os alunos compreenderam com facilidade que só os dígitos depois do ponto

decimal são representados na tabela colorida e sonorizados, pois quando Antonio realizou

a operação 1/1 disseram que nada havia pintado e que não haveria som, pois o número é

inteiro, mas Jéssica logo perguntou: E quando é uma dízima exata? Foi quando realizaram

o próximo número da seqüência ½ e observaram que na tela havia pintado um quadrado

que representava à cor do respectivo dígito depois do ponto decimal, “há pintou um

quadradinho, ai aparece à cor respectiva do número depois da vírgula, cinco”, ao

experimentarem o som, não conseguem conter os risos “tem um som engraçado”, Jéssica

não se contenta e exclama: “Ai que bonitinho!”.

Como os primeiros números da seqüência representam decimais exatos, com

exceção do 1/3, os alunos se mostram apáticos ao realizarem ¼ e 1/5, não se contentam

com a representação dada pela calculadora, pois pinta um ou dois quadradinhos e toca um

o som que acham sem graça, tanto que Antonio se refere à representação sonora do número

1/3 como uma música “é legal quando vem a “musiquinha”, vem fazendo tutututu...

quando vem a dízima periódica”, Jéssica complementa “ela é contínua e não como a exata

que fica o barulhinho” apresentando novamente a característica de infinito da dízima

periódica contrário de um decimal exato que é finito.

Ao realizarem a operação 1/6 notam que algo diferente aconteceu, pois esse

número em sua expansão decimal é uma dízima periódica composta, Jéssica observa que

aparece “só um número diferente dos demais... um só aparece uma vez, ai depois só tem

quadradinho roxo” e Antônio já associa os dígitos com suas respectivas cores “o um é

roxo e o resto é todo amarelo que é 6”. Começam explorar o som e conforme toca a

música observam também no som a mesma diferença obtida na representação visual, toca

uma nota para o dígito 1 e outra nota para o digito 6.

Quando os alunos realizam a operação 1/7 é visível em suas faces uma expressão de

alegria e surpresa diante a pintura obtida pela representação decimal desse número, com

risos Jéssica exclama “ai que bonitinho!”, aprovando a pintura com seis cores vibrantes

obtida pela dízima periódica simples de período 6. Antonio rapidamente se preocupou com

o som que ia ser tocado e curioso perguntou “será que a música vai ficar diferente?...

porque acho que cada número representa uma nota” e ao explorar o som, a expressão de

ambas faces se alegram com o som tocado e em meio de música e risos confirmam as

hipóteses levantadas, criando um laço de afetividade com esse número.

Jéssica referindo-se ao dígito do período tenta explicar porque gostou tanto dessa

representação visual e sonora “que legal... cada número tem uma cor específica e um som

específico, aí dependendo do som você sabe se o mesmo número está contínuo ou se tem

número diferente na seqüência”, mostrando que consegue perceber o período do número

racional tanto na representação visual como sonora.

Pedimos aos alunos para que mudassem a extensão da tabela colorida e durante as

alterações os alunos ficaram curiosos em saber por que as cores estavam ficando alinhadas

(listradas) ou “bagunçadas” como se referiu Jéssica. Começaram a investigar os motivos

dessas alterações na representação visual, pois verificaram que o som sempre era o mesmo

ao ser tocado.

A exploração começou por meio de tentativas, Jéssica propõe a Antonio alterar o

tamanho da tabela colorida começando pelos números pares “tenta usando número par...

tenta por 10 em 10... continua bagunçado, tenta 24 e 48... o dobro fica alinhado”, ao

observar o padrão se repetindo Antonio propõe “vamos tentar com 12... também fica

alinhado... já o 3 não” associando com a seqüência dos múltiplos de 3, mas Jéssica logo

compreende que as cores só ficam alinhadas quando o tamanho da tabela é um número

múltiplo de 6 “tenta 18, 24, 30....de seis em seis ele fica assim (indicando com a mão

colunas) certinho” e Antonio conclui dizendo “ é porque tem seis números aqui...

quatorze, vinte e oito e cinqüenta e sete, quatorze, vinte e oito e cinqüenta e sete”

apontando na tela para 142857 o período de seis dígitos da dízima.

Para finalizar a atividade propomos uma segunda tarefa bem simples, que consistia

em dizer qual dos números da seqüência eles mais se simpatizaram e explicar por quê. A

resposta foi unânime, pois tanto Jéssica como Antonio se simpatizaram pelo mesmo

número, o que não foi surpresa quando disseram o número 1/7 devido à afinidade que

mostraram ao trabalharem com esse número e referiram ao período como uma seqüência

que tem uma representação sonora e visual legal, “1/7 teve aquela seqüência com mais

números, e não ficou aquela coisa repetitiva, o som ... teve diferença tanto na cor quanto

no som”

CONCLUSÕES

A aplicação desse projeto piloto trouxe muitas contribuições para nossa pesquisa.

Na análise parcial dos resultados obtidos no projeto piloto podemos confirmar que alunos

do Ensino Médio possuem dificuldades de compreensão do conceito dos números racionais

e a nova abordagem com a Calculadora Colorida e Musical possibilitou as esses alunos

construir novos significados para esses números.

Podemos identificar na entrevista certa insegurança sobre o conceito dos números

racionais (especialmente Antonio) e uma tendência a privilegiar os números inteiros,

apresentando uma compreensão insatisfatória sobre esse conceito, mas durante a interação

com a calculadora tanto Antonio como Jéssica se mostraram mais seguro, expressando

suas dúvidas e ampliando a compreensão desse conceito.

Na interação com a calculadora, inteiros e decimais exatos, nas palavras dos alunos

são “sem graça”. A calculadora fornece um ambiente no quais as dízimas periódicas são

mais “interessantes”, e os alunos criaram laços mais afetivos com certos tipos de números

o que não aconteceria em um ambiente de aprendizagem com lápis e papel.

A calculadora possibilitou o envolvimento do aluno em investigações matemáticas

como, por exemplo, o que aconteceu para descobrir o período de 1/7, a atenção dos alunos

com a calculadora voltou-se para o que estava acontecendo com os resultados, permitindo

assim a comparação, o levantamento de hipóteses, estabelecimento de relações e

construindo um significado para esse número.

Com relação às narrativas e significado matemático, os alunos criaram narrativas

para interpretar o feedback visual e sonoro – certos números foram descritos com apatia ou

simpatia (alegres) a partir de características particulares e matemáticas (tamanho do

período, tipo de dízima...)

Nestas narrativas estão presentes as características de Bruner, particularmente a

qualidade dramática e conexão entre o extraordinário e o ordinário. Aparentemente essas

narrativas comunicam significados matemáticos que estão começando a associar com

diferentes tipos de número racional.

Como a calculadora está em fase de elaboração, muitas das sugestões indicadas

pelos colegas do curso de Mestrado e dos alunos que participaram do projeto será

implantada, como a questão do infinito que causou preocupação quando o som da

calculadora parou de tocar e a pintura ficou limitada ao quadro, deixando a impressão de

finito.

Da aplicação do projeto surgiram novas idéias à elaboração de atividades para a

próxima etapa. Outras atividades além da descrita foram aplicadas com o objetivo de

organizar alguns números de acordo com as características exploradas com a calculadora e

a partir dessa organização, vamos propor atividades que possibilitam investigação das

propriedades relacionadas entre o denominador e o período da dízima.

A Calculadora Colorida e Musical também abriu possibilidades para a construção

de narrativas, como podemos perceber na interação dos alunos com ela, tornando a

aprendizagem dos números racionais mais significativa e criativa para eles e contribuindo

assim, na busca do entendimento do papel das narrativas na aprendizagem matemática.

Vale lembrar que essa pesquisa tem uma intenção maior, pois abre uma futura

exploração dessa calculadora por alunos surdos (representação visual) e cegos

(representação sonora), por isso a aplicação com alunos regulares contribuirá muito para

que essa possibilidade aconteça.

BIBLIOGRAFIA

BOOTH, W.C. et al. A produção do texto científico - trajetória para sua escrita. São

Paulo: Martins Fontes, 2000.

BRASIL. Ministério da Educação (MEC), Secretaria de Educação Fundamental. PCN:

Matemática. Brasília: MEC/SEF, 1998.

BRUNER, J. Atos de significação. Tradução por Sandra Costa. Porto Alegre: Artes

Médicas, 1997.

DAMICO, A. Uma investigação sobre formação inicial de professores de matemática

para o ensino de números racionais no Ensino Fundamental. Tese de Doutorado. São

Paulo: Puc, 2007.

D’AMBRÓSIO, U. O uso da calculadora. Texto apresentado no Curso a distância da

Sociedade Brasileira de Educação Matemática (SBEM), 2003.

DRISOSTES, T. Ap. Carlos. Design interativo de um micromundo com professores de

matemática do ensino fundamental. Dissertação de Mestrado. São Paulo: PUC, 2006.

HEALY, L. Iterative design and comparison of learning systems for reflection in two

dimensions. Tese de Doutorado. Londres: University de London, 2002.

HEALY, L.; SINCLAIR, N. If this is our mathematics, what are our stories?. International

Journal of Computers for Mathematical Learning Vol. 12 No. 1 pp.3-21. 2007.

KARRER, Mônica. Logaritmos: Proposta de uma seqüência de ensino utilizando a

calculadora. Dissertação de Mestrado. São Paulo: PUC, 1999.

KARRER, Mônica. Articulação entre Álgebra Linear e Geometria: um estudo sobre as

transformações lineares na perspectiva dos registros de representação semiótica. Tese de

Doutorado. São Paulo: PUC, 2006.

SALES, R. O. Cássia; HEALY, L. O Papel das Narrativas Produzidas pelo Aluno na

Aprendizagem Matemática. VIII Encontro de Pesquisa em Educação da Região Sudeste:

Desafios da Educação Básica. Universidade Federal do Espírito Santo, 2007.

SINCLAIR, Nathalie, LILJEDAHL Peter, ZAZKIS Rina. A coloured window on pre-

service teachers’ conceptions of rational numbers. International Journal of Computers for

Mathematical Learning. vol.11, n.2, p. 177-203, 2006.

PAPERT, S. Mindstorm: Children, Computers and Powerful Ideas. London: Harvester

Press, 1980.

PROPOSTA CURRICULAR DO ESTADO DE SÃO PAULO: MATEMÁTICA/ Coord.

Maria Inês Fini. – São Paulo: SEE, 2008.

RIBEIRO, E. V. C. O design e o uso de um micromundo musical para explorar relações

multiplicativas. Dissertação de Mestrado. São Paulo: PUC, 2007.

SOCIEDADE BRASILEIRA DE EDUCAÇÃO MATEMÁTICA PAULISTA. Disponível

em: www.sbempaulista.org.br/epem/anais/Comunicacoes_Orais%5Cco0037.doc -