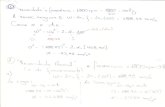Resolução da Lista 8 de FF-207

01. Suponha que a função Hamiltoniana de um sistema de

partículas não varie com uma translação infinitesimal. Discuta a

Conservação do Momentum.

SOLUÇÃO:

Se a função Hamiltoniana não varia com uma translação

infinitesimal, então a coordenada generalizada é cíclica, isto

é, não aparece explicitamente na Hamiltoniana e, portanto

. No entanto, pelas equações canônicas, temos que

. Então, é fácil ver o momento generalizado é

conservado no tempo.

02. Obtenha a função de Hamilton para um oscilador anarmônico,

cuja função de Lagrange é:

SOLUÇÃO:

Da Lagrangeana, segue que:

Com isso, vamos escrever a Hamiltoniana utilizando a

transformação de Legendre:

Sabemos que:

Fazendo as substituições necessárias para eliminar e

acrescentar , temos:

03. Ache a equação de movimento de uma partícula, cuja função de

Hamilton é:

a)

b)

SOLUÇÃO:

a)

As equações canônicas dessa Hamiltoniana são:

Da segunda equação, temos:

Substituindo na primeira:

Elevando-se a segunda equação ao quadrado e substituindo o

valor encontrado acima, temos:

Para não ficar repetindo, vamos chamar

de .

Fazendo a substituição

.

Então, integrando:

Onde

.

b)

As equações canônicas dessa Hamiltoniana são:

Integrando a primeira equação, temos:

Onde é o momento generalizado inicial.

Substituindo na segunda, temos:

Onde é a posição inicial.

Também, podemos fazer de outra forma, mas a equação de

movimento não vai depender explicitamente do .

Isolando na segunda equação e derivando:

Substituindo na primeira equação:

Fazendo

, temos:

Para simplificar os cálculos, vamos chamar

.

Trocando o de novo na equação, chegaremos ao seguinte

resultado:

Onde são respectivamente a posição e a velocidade

inicial.