Collapsing rotating shells in Myers-Perry-AdS5 spacetime:A perturbative approach

Jorge V. Rocha,1,* Raphael Santarelli,2,† and Térence Delsate1,3,‡1CENTRA, Deptartamento de Física, Instituto Superior Técnico, Universidade de Lisboa,

Avenida Rovisco Pais 1, 1049 Lisboa, Portugal2Instituto de Física de São Carlos, Universidade de São Paulo, Caixa Postal 369,

CEP 13560-970 São Carlos, São Paulo, Brazil3Theoretical and Mathematical Physics Department, University of Mons, UMONS,

20, Place du Parc, B-7000 Mons, Belgium(Received 26 February 2014; published 5 May 2014)

We study gravitational perturbations sourced by a rotating test shell collapsing into five-dimensionalMyers-Perry black holes in anti-de Sitter (AdS). Our attention is restricted to the case in which the twopossible angular momenta of the geometry are set equal. In this situation the background is cohomogeneity-1, which amounts to a crucial technical simplification. It is found that the linearized Einstein equations areconsistent only when the test shell is corotating with the spacetime. However, it is argued that this is aconsequence of the matter on the shell being described by dust or, more precisely, noninteracting testparticles. We compute the mass and angular momenta of the perturbed spacetime using a countertermsubtraction method, for which we provide an explicit formula that has not appeared previously in theliterature. The results are in agreement with the expected expressions for energy and angular momenta ofgeodesic particles in AdS5.

DOI: 10.1103/PhysRevD.89.104006 PACS numbers: 04.70.Bw, 04.20.Dw

I. INTRODUCTION

Addressing rotation in the context of general relativity isa notoriously difficult problem. Even when considering anisolated object, rotation deforms bodies away from sphe-ricity, explicitly introducing dependence on polar angles.Conjugated with the nonlinearity of the theory, this basicfact hampers attempts to analytically solve the fieldequations unless some solution-generation technique isapplicable. Just to give an example from black hole (BH)physics, it took roughly half a century to discover therotating generalization [1] of the four-dimensional staticblack hole. Even when considering the linearization arounda given rotating solution, the issue of its stability is far fromtrivial [2].Nevertheless, rotation obviously plays a crucial role in

astrophysical systems. In the axisymmetric gravitationalcollapse of stars the presence of an angular momentum cangenerate centrifugal forces strong enough to prevent theformation of a black hole, leading instead to a bounce. Thisphenomenon has been demonstrated numerically [3,4];generically, there is little analytic control over suchcollapses. A derivation of this effect, by focusing on thedynamics on the equatorial plane, was reported severalyears before in Ref. [5] but it made use of some not entirelyjustified assumptions.

There is by now a vast literature on the subject ofgravitational collapse, but it is almost entirely dedicated tospherically symmetric scenarios (see, e.g., [6]). The sit-uation concerning collapse with rotation is much lessdeveloped. A very useful approach, due to its simplicity,is to consider collapsing shells of matter but, even so, theinclusion of rotation typically impedes a full analytictreatment of the problem. A few exceptions are providedby Refs. [7,8], which rely on a slow rotation approximation.More recently, an interesting study by Mann et al. [9] wasable to tackle the problem exactly, at the expense ofconsidering three spacetime dimensions.In this paper we investigate gravitational perturbations

induced by a collapsing shell of test particles into a rotatingblack hole in five dimensions, with a negative cosmologicalconstant. This is the same approach adopted in [10], whereperturbations of the three-dimensional rotating black holein anti-de Sitter (AdS) by an infalling circular ring of testparticles were examined. Here, however, we shall perturbthe BH spacetime with a continuous test shell preserving allthe angular symmetry of the five-dimensional background.In higher dimensions there can be several independentangular momenta [11]. We take advantage of the fact that,in odd dimensions (D ≥ 5), when all the angular momentaare equal—and we restrict to this case—the rotating blackhole geometry is cohomogeneity-1 [12], allowing us todescribe the solution by functions of only one coordinate.The black hole event horizon and all constant radialsurfaces are topologically odd-dimensional spheres. Suchspaces can be endowed with metrics that break isotropy but

*jorge.v.rocha@tecnico.ulisboa.pt†santarelli@ifsc.usp.br‡terence.delsate@umons.ac.be

PHYSICAL REVIEW D 89, 104006 (2014)

1550-7998=2014=89(10)=104006(13) 104006-1 © 2014 American Physical Society

preserve homogeneity, and this was fruitfully used inRef. [13] to study vacuum gravitational collapse withrotation but in a numerically less-demanding scenario.For simplicity, we will consider the five-dimensional case,but, as discussed in Sec. V, we expect that our results maygeneralize to higher odd dimensions without much effort.Our study can be regarded as an extension of an analysis

by Zerilli (see Appendix G of Ref. [14]) to higherdimensions and by the addition of two more parameters(rotation and the cosmological constant). In the nonrotatingcase the metric perturbation can be expanded in higher Dspherical harmonics, which all decouple in the linearizedEinstein equations, and our results describe the solution ofthe lowest harmonic, i.e., monopole perturbation. However,for the nonvanishing spin of the background, the equationsno longer decouple and our solution cannot be expected todescribe the projection of the perturbed metric onto thelowest angular harmonic (zero mode) when the sourcebreaks the angular symmetry of the background.The motivation for such a study is at least twofold. First,

the analysis of linearized perturbations allows us, inprinciple, to identify the “energy” and “angular momen-tum” of a rotating test shell in five-dimensional, asymp-totically AdS spacetimes. This in turn determines thevariation of the charges of the spacetime caused by eachpoint particle. Such knowledge is essential to perform testsof the cosmic censorship conjecture [15] in such space-times, by attempting to overspin extremal rotating blackholes with point particles as envisaged originally by Wald[16] and extended recently to higher dimensions inRef. [17], and to spacetimes with a cosmological constantin Refs. [10,18,19].On the other hand, gravitational collapse in AdS space-

times has important implications for thermalization ofstrongly coupled conformal field theories (CFTs) via thegauge-gravity duality (see [20] for a review). In Ref. [21]the fast thermalization process of a CFT (on a sphere)perturbed away from the vacuum by a homogeneous shortpulse was inferred by following the spherically symmetriccollapse of a scalar field into a black hole in the holographicdual setting (see [22,23] for related numerical works). It isnaturally desirable to know whether the inclusion ofrotation has some impact on this picture, as all of thesestudies rely on spherical symmetry. We take a first step inthis direction by computing the one-point function of theholographically dual stress-energy tensor, following thecounterterm subtraction proposal of Ref. [24].The outline of the paper is as follows. In the next section

we briefly present the black hole geometries we shallconsider. In Sec. III we discuss the linearized Einsteinequations, the geodesics on this spacetime, and the stress-energy tensor the test particles generate. These linearizedperturbation equations are then solved in Sec. IV and theresult is used to determine the variation of the mass andangular momentum of the spacetime caused by the test

particles. We conclude in Sec. V with some discussion andremarks. The appendixes gather several technical detailsconcerning gauge fixing and solving the gravitationalperturbation equations.

II. EQUALLY SPINNING BLACK HOLESIN FIVE DIMENSIONS

In this section we gather the relevant details about five-dimensional rotating black holes with a negative cosmo-logical constant when both angular momenta are equal.These spacetimes will serve as a background on top ofwhich we analyze linear perturbations in Sec. IV. Theseblack hole solutions in AdS5 were first presented in [25]and have been extended to arbitrary dimensions D ≥ 4 in[26,27], thus generalizing the well-known Myers-Perryfamily [28] to include a cosmological constant.In five spacetime dimensions one can pick two orthogo-

nal planes of rotation. In general, the solution is para-metrized by two independent angular momenta a1 and a2,in addition to a mass parameterM. As shown in [12], whenthe rotation parameters are set equal, a1 ¼ a2 ¼ a, theisometry group gets enhanced and the solution becomescohomogeneity-1. The geometry essentially depends on asingle radial coordinate only, and the metric can be writtenas follows:

ds2 ¼ −fðrÞ2dt2 þ gðrÞ2dr2 þ r2gabdxadxb

þ hðrÞ2½dψ þ Aadxa −ΩðrÞdt�2; (1)

where

gðrÞ2 ¼�1þ r2

l2−2GMΞr2

þ 2GMa2

r4

�−1; (2)

hðrÞ2 ¼ r2�1þ 2GMa2

r4

�; ΩðrÞ ¼ 2GMa

r2hðrÞ2 ; (3)

fðrÞ ¼ rgðrÞhðrÞ ; Ξ ¼ 1 −

a2

l2: (4)

In the above expressions gab represents the Fubini-Studymetric on the complex projective space CP1, which isisomorphic to the sphere S2, and A ¼ Aadxa is its Kählerpotential:

gabdxadxb ¼1

4ðdθ2 þ sin2θdϕ2Þ; A¼ 1

2cosθdϕ: (5)

The above form of the metric (1) extends to all higherodd dimensionsD ¼ 2N þ 3 [12]: this is made possible bythe fact that the sphere S2Nþ1 can be written as an S1 bundleover CPN. For the case D ¼ 5 on which we concentrate,this corresponds to the familiar Hopf fibration. Thecoordinate ψ parametrizes the S1 fiber and has the period2π. The two orthogonal rotation planes correspond to θ ¼ 0

ROCHA, SANTARELLI, AND DELSATE PHYSICAL REVIEW D 89, 104006 (2014)

104006-2

and θ ¼ π in these coordinates, i.e., the rotation planes aremapped to the poles of the S2.This metric is a solution of the Einstein equations with a

negative cosmological constant,

Rμν ¼ −4l−2gμν: (6)

The largest real root, rþ, of g−2 marks an event horizon thatpossesses the geometry of a homogeneously squashed S3

(written above as its Hopf fibration). The mass M andangular momentum J of the spacetime are given by [12]

M ¼ πM4G

�3þ a2

l2

�; J ¼ πMa

G: (7)

In the expressions above and in the rest of the manu-script, we will use natural units, normalizing the speed oflight to c ¼ 1, but we shall explicitly keep factors of theNewton constant G.

III. LINEARIZED GRAVITATIONALPERTURBATIONS

We are interested in investigating the consequences ofperturbing the background spacetime by a (comparativelylight) infalling membrane of test particles homogeneouslydistributed on the squashed S3. The meaning of this will bemade precise in Sec. III A. For now we just remark that thissituation preserves the full rotational symmetry of thebackground [29], and, in particular, the equal angularmomentum property. Of course, stationarity is lost dueto the presence of the infalling test particles.For this study, we will adopt the framework of linearized

perturbations. The perturbed metric is obtained from thebackground metric gμν by

~gμν ¼ gμν þ hμν: (8)

As mentioned previously, the background metrics we shallconsider are solutions of the sourceless cosmologicalEinstein equations in five dimensions and reads

Gcμν ≡Gμν −

6

l2gμν ¼ 0: (9)

Here, Gμν ¼ Rμν − 12gμνR denotes the Einstein tensor, Λ≡

−4=l2 represents the (negative) cosmological constant, andl is the AdS radius. The linearized perturbation equationsderived from (9) are the following [30,31]:

2δGcμν ≡ −∇2hμν þ 2∇λ∇ðμhνÞλ −∇μ∇νh

þ gμνð∇2h −∇α∇βhαβÞ − hμνR

þ gμνhαβRαβ − 12l−2hμν

¼ 16πGTμν; (10)

where covariant derivatives are taken with respect to thebackground metric and h≡ gμνhμν denotes the trace ofthe metric perturbation. Tμν is the stress-energy tensor ofthe test particles that will drive the perturbation. By virtueof the Bianchi identity, the stress-energy tensor must bedivergenceless to ensure consistency of equations (10).This occurs if and only if the source particles followgeodesics. These equations easily generalize to higherspacetime dimensions.Particularizing to the background vacuum solution (1),

the linearized perturbation equations become

−∇2hμνþ2∇λ∇ðμhνÞλ −∇μ∇νhþ gμνð∇2h −∇α∇βhαβÞ

þ 8l−2�hμν −

1

2gμνh

�¼ 16πGTμν: (11)

In Sec. III B we will determine the generic form of thestress-energy tensor for a shell of test particles thatpreserves all of the angular isometries of the background.As usual, diffeomorphism invariance of the theory

implies the existence of gauge freedom that can be usedto eliminate some terms appearing in the differentialoperator on the left-hand side of Eq. (11). Typically, thechoice of transverse traceless gauge is made, reducing thedifferential operator to the Lichnerowicz operator.However, the expected form of the perturbation, i.e., oneleading to a shift of the mass and rotation parameters,

M → M þ δM; a → aþ δa; (12)

in the region outside the shell is not consistent with suchgauge fixing. We will find it more convenient to make adifferent gauge choice, one that preserves the symmetry ofthe background. This is discussed in Appendix A.

A. Conserved quantities and geodesics

Consider a test particle moving along some geodesic ofthe spacetime (1). The world line is described byzμðτÞ ¼ ðTðτÞ; RðτÞ;ΨðτÞ;ΘðτÞ;ΦðτÞÞ, where τ is an affineparameter. A rotating stationary spacetime specified by ametric tensor gμν possesses both time-like and rotationalKilling vectors, from which we can build three conservedquantities,

E≡ −gμν∂tμ _zν ¼ −

dTdτ

�gtt þ gtψ

dΨdT

þ gtϕdΦdT

�; (13)

Lψ ≡ gμν∂ψμ _zν ¼ dT

dτ

�gtψ þ gψψ

dΨdT

þ gψϕdΦdT

�; (14)

Lϕ ≡ gμν∂ϕμ _zν ¼ dT

dτ

�gtϕ þ gψϕ

dΨdT

þ gϕϕdΦdT

�; (15)

where the dot indicates derivation with respect to τ.

COLLAPSING ROTATING SHELLS IN MYERS-PERRY-ADS … PHYSICAL REVIEW D 89, 104006 (2014)

104006-3

Now, note that

gtϕ ¼ cos θ2

gtψ ; gψϕ ¼ cos θ2

gψψ ;

gϕϕ ¼ cos θ2

gψϕ þr2sin2θ

4; (16)

so a test particle whose motion lies entirely in the rotationplane θ ¼ 0 has Lϕ ¼ 1

2Lψ . Similarly, a test particle whose

motion lies entirely in the rotation plane θ ¼ π hasLϕ ¼ − 1

2Lψ . These geodesics satisfy

_ΘðτÞ ¼ _ΦðτÞ ¼ 0: (17)

In fact, there exist geodesics obeying (17) for any valueof θ and ϕ. Such geodesics simply correspond to statictrajectories on the S2 and they have

Lϕ ¼ cos θ2

Lψ : (18)

Thus, to preserve the most amount of symmetry of thebackground, in this work we will consider a membrane oftest particles homogeneously smeared over the S2, witheach point particle infalling radially. The particles will alsobe homogeneously distributed over the S1 but they willpossess some rotation along the ψ direction (see Fig. 1).The remaining equations governing the test particle

trajectories are easily obtained by inverting (13) and (14)and using gμν _zμ _zν ¼ −ϵ to obtain the radial equation

_T ¼ E − ΩLψ

f2; (19)

_Ψ ¼ h2ΩEþ ðf2 − h2Ω2ÞLψ

h2f2; (20)

_R2 ¼ −ϵ − f−2½E −ΩLψ �2 þ h−2L2

ψ

g2; (21)

where ϵ ¼ 1, 0 for time-like or null geodesics, respectively.In these equations the metric functions f, g, h, Ω should allbe considered as functions of RðτÞ instead of r.In this work we will restrict to the case ϵ ¼ 0, corre-

sponding to null geodesics that reach the time-like boun-dary of AdS. Although it is not immediately clear how toseparately define the black hole and the test particle whenthe latter cannot be moved all the way out to time-likeinfinity, one can nevertheless compute the effect that theintroduction of a test particle in the background geometryhas on the energy and angular momenta of the spacetime.This will be done in Sec. IV.

B. The stress-energy tensor

For a single point particle of rest mass m0, the stress-energy tensor is given by [14]

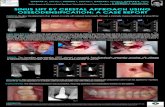
FIG. 1 (color online). Geodesics followed by individual test particles shown in arrowed red lines. The left panel shows the pointparticle trajectories projected onto the three-dimensional space parametrized by spherical coordinates ðr; θ;ϕÞ. The trajectories in thisspace are radial. The right panel illustrates similar trajectories now projected onto the two-dimensional space parametrized by polarcoordinates ðr;ψÞ. In both panels the location of the black hole event horizon, in black, and of the continuous shell of test particles at asnapshot in time, in grey, are superimposed.

ROCHA, SANTARELLI, AND DELSATE PHYSICAL REVIEW D 89, 104006 (2014)

104006-4

TμνðppÞ ¼ m0

Zδð5Þðx − zðτÞÞ dz

μ

dτdzν

dτdτ; (22)

where, recall, τ denotes an affine parameter along theworldline zμðτÞ.As mentioned before, we will perturb the background

spacetime with test particles homogeneously (and contin-uously) distributed over both the S1 and S2. The stress-energy tensor will thus be a function of the coordinates tand r only, and it can be computed by a simple change ofvariables. After performing the time integral and thenintegrating over the angular coordinates (to yield Tμν

ðppÞsmeared over the squashed S3), we obtain [14,32]

Tμν ¼ 4m0ϑμν δðr − RðtÞÞ

r3; ϑμν ≡ dT

dτdzμ

dtdzν

dt: (23)

For massive particles, the quantity m0 appearing in (23) isthe mass density of the test shell. For massless particles theform (22) for the stress-energy tensor is still valid [30] butthe parameter m0 should then be interpreted as an energydensity throughout the shell. The covariant components ofthe stress-energy tensor may be expressed as follows:

ϑtt ¼ −E�gtt þ gtψ

dΨdt

�; ϑtr ¼ −Egrr

dRdt

;

ϑtψ ¼ −E�gtψ þ gψψ

dΨdt

�; ϑrr ¼

dTdτ

g2rr

�dRdt

�2

;

ϑψψ ¼ Lψ

�gtψ þ gψψ

dΨdt

�; ϑrψ ¼ Lψgrr

dRdt

;

ϑtϕ ¼ −E�gtϕ þ gψϕ

dΨdt

�; ϑrϕ ¼ Lϕgrr

dRdt

;

ϑψϕ ¼ Lψ

�gtϕ þ gψϕ

dΨdt

�; ϑϕϕ ¼ Lϕ

�gtϕ þ gψϕ

dΨdt

�:

(24)

The components ϑμθ all vanish. This stress-energy tensor istraceless (Tμ

μ ¼ 0) and conserved (∇μTμν ¼ 0), as isimposed by the Bianchi identities. Note that, using therelations

−E�gtψ þ gψψ

dΨdt

�¼ Lψ

�gtt þ gtψ

dΨdt

�; (25)

−E�gtϕ þ gψϕ

dΨdt

�¼ Lϕ

�gtt þ gtψ

dΨdt

�; (26)

Lψ

�gtϕ þ gψϕ

dΨdt

�¼ Lϕ

�gtψ þ gψψ

dΨdt

�; (27)

one can express ϑtψ in terms of Lψ and both ϑtϕ and ϑψϕ interms of Lϕ.

IV. SOLVING THE LINEARIZEDPERTURBATION EQUATIONS

In this section we will solve the perturbation equa-tions (11), with the stress-energy tensor given by Eq. (23).To this end, we begin by gauge fixing so that the metric

perturbation hμν takes a convenient form, similar to thatdictated by a (time-independent) shift of mass and angularmomentum. Several perturbation components automati-cally vanish, which simplifies the process of solving theperturbation equations. Having a solution, we may theninfer the effect the test shell has on the spacetime, namelyby determining the change in the mass δM and in theangular momentum δJ imputed on the background. Thiswas essentially the same strategy followed in the muchsimpler ð2þ 1Þ-dimensional case [10]. A similar approachis followed in Ref. [31], though with a different problemin mind.We will first consider the fully nonrotating case, where

the background is static and the test shell infalls radially.This is a instructive limit because it can be solved fullyanalytically and builds up some intuition for the rotatingcase, which we address in a separate subsection.In Appendix A it is shown that the metric perturbation

can be gauge fixed into the following form, possessing onlyfour independent components:

hμν ¼

2666664

htt 0 htψ 0 cos θ2

htψ0 gðrÞ4hrr 0 0 0

� 0 hψψ 0 cos θ2

hψψ0 0 0 0 0

� 0 � 0 cos2θ4

hψψ

3777775: (28)

A factor of gðrÞ4 is inserted in the frrg component forconvenience.Therefore, we have a total of fifteen equations to solve

for only four functions (of t and r). Not all of Eqs. (11) arelinearly independent. In fact, there is only one dynamicalequation that determines one of the nontrivial perturbationcomponents, say hψψ. The other components are fixed byconstraint equations. This is in agreement with the appen-dix of reference [31].

A. The nonrotating case

In the nonrotating case (a ¼ 0 and Lψ ¼ 0) one can infact gauge fix so that htψ ¼ hψψ ¼ 0 (see Appendix A).The metric perturbation has only two nontrivial compo-nents: htt and hrr.As mentioned above, in this special case one can solve

the linearized perturbation equations exactly. The systemof fifteen equations reduces to just four equations, corre-sponding to components fttg, ftrg, frrg,

COLLAPSING ROTATING SHELLS IN MYERS-PERRY-ADS … PHYSICAL REVIEW D 89, 104006 (2014)

104006-5

3ðr4 þ l2r2 − 2Ml2Þl2r5

∂r½r2hrr� ¼64πm0Eðr4 þ l2r2 − 2Ml2Þ

l2r5δðr − RðtÞÞ; (29)

3l2rr4 þ l2r2 − 2Ml2

∂thrr ¼ −64πm0El2R0ðtÞ

rðr4 þ l2r2 − 2Ml2Þ δðr − RðtÞÞ; (30)

3l2

�2r2ðl2 þ 2r2Þ

ðr4 þ l2r2 − 2Ml2Þ2 hrr þ1

r∂r

�r2htt

r4 þ l2r2 − 2Ml2

��¼ −

64πm0l4rR0ðtÞ2 _Tðr4 þ l2r2 − 2Ml2Þ2 δðr − RðtÞÞ; (31)

in addition to a longer and not so enlightening equation from the fψψg component, which we avoid presenting. Theremaining equations are either trivially satisfied or linearly dependent on the former. It is straightforward to solve the system(29)–(31) and the final result is

httðt; rÞ ¼C1

r2−r4 þ l2r2 − 2Ml2

3l2r2C2ðtÞ þ

64πm0E3r2

Θðr − RðtÞÞ�1 − 2

r4 þ l2r2 − 2Ml2

RðtÞ4 þ l2RðtÞ2 − 2Ml2

�; (32)

hrrðt; rÞ ¼C1

r2þ 64πm0E

3r2Θðr − RðtÞÞ: (33)

Here, C1 is a constant and C2 represents an arbitraryfunction of t. We have used Eq. (19) to replace _T in (31). Itcan be checked that this solution also satisfies the remain-ing independent equation arising from the fψψg compo-nent. The solution for the asymptotically flat case can beeasily obtained by taking the l → ∞ limit.Some comments regarding the solution (32)–(33) are

now in order. The terms not proportional to m0 areobviously not sourced by the test particles. The termsproportional to C1 correspond to a simple (static) pertur-bation of the mass parameter. On the other hand, the time-dependent term C2ðtÞ can be gauged away by using theresidual gauge freedom discussed in Appendix A. Thus, wemay set C1 ¼ C2ðtÞ ¼ 0. The component hrr then takesexactly the form that would be expected: it is proportionalto r−2 and to the Heaviside function Θðr − RðtÞÞ. The fttgcomponent, on the other hand, is more involved, thoughstill proportional to Θðr − RðtÞÞ. It appears to grow as r2,but this is again a gauge artifact. The residual gaugefreedom can also be used to eliminate the entire secondterm inside the square brackets in Eq. (32), at the expenseof introducing some nontrivial behavior for r < RðtÞ.Stated differently, if we completely gauge fix by requiringthe metric perturbations to decay as r → ∞, then htt ¼hrr ¼ Oðr−2Þ for r > RðtÞ. In that case, htt ¼ hrr forr > RðtÞ, although htt then acquires nontrivial supportinside the test shell.Nevertheless, it is the hrr component that determines the

mass of the spacetime. This can be computed using thequasilocal stress tensor formalism of Ref. [24], which relieson a counterterm subtraction method. For an asymptoticallyAdS5 spacetime, the required counterterms to render theboundary stress tensor finite have been identified in [24], towhich we refer for details of the computation. A long but

straightforward calculation reveals that the variation in themass of the spacetime is given by

δM ¼ limr→∞

3

64πG

Z2π

0

dϕZ

2π

0

dψZ

π

0

dθ sin θ

×

�r2hrr − ðl2 þ 8MÞl

2htt8r2

�¼ 8π2m0E

G; (34)

i.e., it is determined by the net energy m0E of the testparticles (the factor of 8π2 accounts for the integration ofthe continuous distribution over the 3-sphere).We conclude that the test shell in this nonrotating setting

has the effect (at linear level) of adding an energy8π2m0E=G to the background spacetime.

B. The rotating case

In the fully rotating case we have four functions of t andr to solve for. The linearized Einstein equations are verylengthy but can be reduced to a system of four equations(see Appendix B): a decoupled second order partial differ-ential equation (PDE) for hψψ , a coupled ordinary differ-ential equation (ODE) that determines htψ once hψψ isgiven, and two constraint equations that fix hrr and htt oncethe other two nontrivial components are known. In therotating case the nonhomogeneous PDE for hψψ does notseem possible to solve in closed form. Nevertheless, onecan find a solution in the form of an asymptotic expansionin powers of 1=r and 1=RðtÞ near the boundary of AdS.This is in fact all we need to compute the conserved chargesof the test shell.Given the general form of the differential equations

being solved—with source terms proportional to deltadistributions and step functions—we seek solutions ofthe form

ROCHA, SANTARELLI, AND DELSATE PHYSICAL REVIEW D 89, 104006 (2014)

104006-6

hμνðt; rÞ ¼ ημνðRðtÞ; rÞΘðr − RðtÞÞ; (35)

for some tensor field ημνðRðtÞ; rÞ.This is also what is expected on physical grounds:

perturbations preserving the full Uð2Þ spatial symmetryof the background vanish inside the shell, modulo aresidual gauge freedom similar to the nonrotatingcase. Inserting this ansatz in Eqs. (B1)–(B4), we obtaina system of differential equations coming from the termsproportional to Θðr − RðtÞÞ, which are supplemented by aset of boundary conditions stemming from the termsproportional to δðr − RðtÞÞ and δ0ðr − RðtÞÞ (seeAppendix C).

Let us focus on the decoupled equation (B1) governingthe component hψψ . Application of the ansatz (35) returns along nonhomogeneous second order PDE for ηψψ. It can beshown that

ηðpÞψψ ðrÞ ¼ 32πm0l2að2aE − 3Lψ Þða2 − 3l2Þr2 (36)

is a particular solution of this nonhomogeneous equation. Aclose examination reveals that the associated homogeneousequation is separable, ηψψðR; rÞ ¼ ΣðRÞσðrÞ. The solutionsfor each of the two functions σ and Σ can be expressed in anasymptotic power series in 1=r and 1=RðtÞ, respectively,and the result is

ηðhÞψψðR; rÞ ¼Z

∞

0

dκαðκÞ�1

r2þ κ2l4

12r4þ −128a2M þ 384l2M − 28l6κ2 þ l8κ4

384r6þOðr−8Þ

�

×

�1þ κ2E2l6

2ðE2l2 − L2ψ ÞR2

þ κ2E2l8ðE2l2ðl2κ2 − 8Þ þ 12L2ψ Þ

24ðE2l2 − L2ψÞ2R4

þOðR−6Þ�: (37)

Here, the integration variable κ is the separability constant and the integration stems from the basic fact that any linearcombination of solutions—parametrized by κ—will also give a solution to the homogeneous equation. Defining

Ai ≡Z

∞

0

dκκ2iαðκÞ; i ¼ 0; 1; 2;…; (38)

we may write the general asymptotic solution as

ηψψðR; rÞ ¼32πm0l2að2aE − 3LψÞ

ða2 − 3l2Þr2 þ A0

r2þ A1l4

12r4þ A1E2l6

2ðE2l2 − L2ψ Þr2R2

−A0ða2 − 3l2ÞM

3r6−7A1l6

96r6

þ A2l8

384r6þ A2E2l10

24ðE2l2 − L2ψÞr4R2

−A1E2l8ð2E2l2 − 3L2

ψÞ6ðE2l2 − L2

ψÞ2r2R4þ A2E4l12

24ðE2l2 − L2ψ Þ2r2R4

þ…; (39)

where the dots refer to higher order terms in 1=r and 1=Rthat when evaluated at r ¼ RðtÞ become OðR−8Þ.The constraint (C3) yields the simple boundary condition

L2ψηψψðR;RÞ¼0. IfLψ ≠ 0 this fixes the parametersAi to be

A0 ¼ −32πal2m0ð2aE − 3LψÞ

ða2 − 3l2Þ ; (40)

A1 ¼ 0; (41)

A2 ¼ −4096πaMm0ð2aE − 3Lψ ÞðE2l2 − L2

ψ Þ2l6ð33E4l4 − 18E2l2L2

ψ þ L4ψ Þ

: (42)

Thus, the solution at this point takes the simpler form

ηψψðR; rÞ ¼ −512πaMl4m0E2

3r6R4ðr2 − R2Þð2aE − 3Lψ Þ

×E2l2ðr2 þ 2R2Þ − R2L2

ψ

33E4l4 − 18E2l2L2ψ þ L4

ψþ…: (43)

To complete the determination of hψψ we must also imposetheboundaryconditions (C4)and(C5).Plugging thesolution(43) in either (C4) or (C5) returns an equation of the form

m0L2ψYðRÞ ¼ 0; (44)

whereYðRÞ isanunenlighteningrational functionofR.Sotheboundary conditions can only be satisfied—for genericvalues of the radial position of the test shell—if Lψ ¼ 0(assuming m0 ≠ 0, otherwise there would be no test par-ticles). In this case the asymptotic solution (39) satisfyingboundary conditions (C4) and (C5) turns out to be

ηψψðR; rÞ≃ −1024πa2Ml2m0Eðr4 þ r2R2 − 2R4Þ

99r6R4;

(45)

which can equally be obtained by taking the limit Lψ → 0in (43).

COLLAPSING ROTATING SHELLS IN MYERS-PERRY-ADS … PHYSICAL REVIEW D 89, 104006 (2014)

104006-7

We conclude that, in general, the (hyperbolic) PDE forthe component hψψ has no nontrivial solution satisfyingthe boundary conditions. The only consistent case isLψ ¼ 0, for which an asymptotic solution can indeed befound. In other words, a shell of perfect fluid dustpreserving the full spatial symmetry of the backgroundbut not corotating with the spacetime is inconsistentwith the linearized Einstein equations. Thus, we restrictto Lψ ¼ 0 in the remainder of this section. It is easy to seefrom Eq. (21) that in this case the motion of the (null) test

shell indeed describes a full collapse, i.e., a bounce neveroccurs.Following the same strategy, we can now straightfor-

wardly compute the remaining nontrivial metric perturbationcomponents by integrating Eqs. (B2)–(B4). In doing so, wemust keep terms up to the order Oðr−6Þ, including termsup to order r−4OðRðtÞ−2Þ, r−2OðRðtÞ−4Þ, OðRðtÞ−6Þ, andr2OðRðtÞ−8Þ, which contribute at the same order whenimposing the boundary conditions at r ¼ RðtÞ. The finalresult is

hψψðt; rÞ≃ −1024πa2Ml2m0E

99Θðr − RðtÞÞ r

4 þ r2RðtÞ2 − 2RðtÞ4r6RðtÞ4 ; (46)

htψðt; rÞ≃ 128πaMl2m0E3

Θðr − RðtÞÞ r4 − RðtÞ4r2RðtÞ8 ; (47)

hrrðt; rÞ≃ 64πm0E3r2

Θðr − RðtÞÞ�1þ 32a2M

2r2 þ 3RðtÞ299r2RðtÞ4

�; (48)

httðt; rÞ≃ 64πm0E3r2

Θðr − RðtÞÞ�1 − 2

r4 þ l2r2 − 2Ml2

RðtÞ4 þ a2M99

�16

RðtÞ4 −34

r4−396r2ðr2 þ l2Þ

RðtÞ8��

: (49)

This is in full agreement with the exact result obtainedfor the nonrotating case: this asymptotic solution reduces toEqs. (32) and (33) when a ¼ 0 (up to the higher ordercorrections in powers of RðtÞ−1). Observe that we cannottake the flat limit l → ∞ consistently from the aboveasymptotic solution: terms of subleading order in powers ofRðtÞ—which are being discarded in Eqs. (46)–(49)—willgenerically introduce extra factors of l.In writing the above solution we have set some integra-

tion constants to zero in order to retain only the part sourcedby the test shell that interests us. Expressions (46) and (48)

explicitly show that hψψ and hrr both decay as r−2. As inthe nonrotating case, here we can also resort to the residualgauge freedom to eliminate the Oðr2Þ terms that appear in(47) and (49), at the expense of introducing nontrivialbehavior for r < RðtÞ (see Appendix A). It turns out thatafter performing this residual gauge fixing the componenthtψ becomes of the order Oðr−4Þ.Adopting the quasilocal stress tensor approach of [24],

these linear perturbations determine the variation of themass and angular momentum of the spacetime, which aregiven by

δM ¼ limr→∞

1

64πG

Z2π

0

dϕZ

2π

0

dψZ

π

0

dθ sin θ

�3r2hrr þ

2r2

l2hψψ −

r3

l2∂rhψψ−

3l4 þ 24l2M þ 8a2M8r2

htt

�¼ 8π2m0E

G;

(50)

δJ ψ ¼ limr→∞

1

64πG

Z2π

0

dϕZ

2π

0

dψZ

π

0

dθ sin θ ½2r2htψ − r3∂rhtψ � ¼ 0: (51)

Note that the result for the increment in mass is thesame as in the nonrotating case, Eq. (34): the finite terms(in the limit r → ∞) coming from hrr that are proportionalto a2M exactly cancel the contribution from hψψ . Thevariation in the angular momentum vanishes, asexpected, since we considered a corotating test shell.To be precise, the quantity computed in Eq. (51) is thechange in the ψ−component of the angular momentumof the spacetime—the only component that is initially

nonzero. The variations of the other two angular compo-nents trivially vanish.In the spirit of holographic renormalization, the bulk

coordinates are naturally split as xμ ¼ ðr; xiÞ, withxi ¼ ðt;ψ ; θ;ϕÞ, and the radial coordinate r is interpretedroughly as an inverse energy scale from the dual fieldtheory point of view. The quantities computed above aresimply proportional to the fttg and ftψg components of theone-point function of the (perturbed) dual stress-energy

ROCHA, SANTARELLI, AND DELSATE PHYSICAL REVIEW D 89, 104006 (2014)

104006-8

tensor. More generally, the expectation value of theboundary stress-energy tensor is dictated, via the quasilocalstress tensor T ij, by the asymptotic behavior of the metric[23,24]:

hTijðxkÞi ¼ limr→∞

r2T ijðr; xkÞ: (52)

We refer the reader to [24] for the explicit expression of thequasilocal stress tensor.For completeness, we present the results for the pertur-

bation induced by the collapsing test shell on the one-pointfunction of the boundary stress-energy tensor:

hδTtti ¼4m0EGl

; (53)

hδTψψi ¼4m0El3G

�1 −

128a2M99RðtÞ4

�; (54)

hδTψϕi ¼cos θ2

hδTψψi; (55)

hδTθθi ¼m0El3G

�1þ 64a2M

99RðtÞ4�; (56)

hδTϕϕi ¼cos2θ4

hδTψψ i þ sin2θhδTθθi: (57)

All other components of hδTiji not related by symmetryvanish. This calculation also uncovers an interesting effect:although the actual radial location of the test shell does notinfluence the energy and momentum density, there is anexplicit dependence on RðtÞ in the spatial components,which corresponds to pressures and shear.

V. DISCUSSION

In this work we have studied the collapse of a rotatingshell of null test particles towards a five-dimensionalrotating black hole in asymptotically AdS spacetime withequal rotation parameters. We employed a perturbativeapproach by considering the aforementioned black holegeometry as a fixed background, and studying the (linear-ized) effects of a test shell preserving all the rotationalsymmetry of the spacetime.We first considered the nonrotating case, which is

instructive because the linearized Einstein equations canbe solved exactly. The presence of the shell increases thetotal energy of the spacetime by an amount precisely equalto the mass of the shell. For the fully rotating case, we wereonly able to solve the perturbation equations asymptoti-cally. Nevertheless, this was sufficient to show that theintroduction of a continuous and homogeneous distributionof (noninteracting) test particles preserving the Uð2Þsymmetry of the equally rotating Myers-Perry-AdS5 back-ground is only consistent if the angular momentum

parameter of the particles vanishes, Lψ ¼ 0, i.e., if theshell is corotating with the background.In practice, the noninteracting character of the test

particles constituting the shell, which is sourcing theperturbations, translates into the shell equation of statebeing that of dust. The above conclusion implies that, if wewant to consider a general Lψ ≠ 0 case, we must add extraterms to the stress-energy tensor to alter the angularmomentum of the black hole. Roughly speaking, theperfect fluid form of the stress-energy tensor does notcarry the appropriate charge to affect the spin of the blackhole, and consistency of the linearized Einstein equationsfor Lψ ≠ 0 requires the introduction of additional forces.The angular momentum of the test shell should be given byan off diagonal element of the stress-energy tensor, namelyTtψ . So one expects that at least some momentum flux isneeded for consistency. This is indeed confirmed by anexact treatment that will be presented elsewhere [33].It seems very likely that our results for the five-dimen-

sional equally spinning Myers-Perry-AdS black hole gen-eralizes to all odd higher dimensions, since the structure ofthe linearized equations remains unaltered. In particular,there should still be four independent equations governingthe perturbations, even though the total number of degreesof freedom grows as D2. This is a consequence of the highdegree of symmetry we impose on the perturbed spacetime.The specific case we studied has equal angular momenta inthe two independent rotation planes but in less symmetricsituations we expect similar results [34]. In particular, a thindust shell in such a spacetime must be corotating; other-wise, it must be composed of a nonperfect fluid.As a byproduct of our studies, we derived explicit

expressions for the change in mass and angular momentumof these spacetimes induced by the test shell though thegravitational perturbations it sources. The countertermprescription we adopted [24], also known as the quasilocalstress tensor formalism, reproduces the expected results. Inany case, the expressions obtained, Eqs. (50) and (51), aregenerically valid for gravitational perturbations of thesespacetimes that preserve the background angular symmetryand its AdS asymptotics. This provides a hint that thisprocedure may also give consistent results in a nonlinearsituation, e.g., a backreacted collapse or BH collision inAdS, provided the gauge is suitably chosen, namely that thespacetime is asymptotically locally AdS.A point worth mentioning is related to the explicit time

dependence in the asymptotic solution found for therotating case, Eqs. (46)–(49). As discussed in [13,35],even though the full angular symmetry of the background ispreserved by the perturbations considered, the Birkhoff-Jebsen theorem can be evaded in odd dimensions.Therefore, the spacetime outside the test shell need notbe static, or even stationary, as it turns out to be the case.In this investigation we have resorted to gauge fixing in

order to solve the perturbation equations. Alternatively, we

COLLAPSING ROTATING SHELLS IN MYERS-PERRY-ADS … PHYSICAL REVIEW D 89, 104006 (2014)

104006-9

could have chosen to work with a gauge-invariant formu-lation, as done in Ref. [31] to study sourceless perturba-tions. It would be interesting to extend that technology tononvacuum perturbations.

ACKNOWLEDGMENTS

We thank Vitor Cardoso and Jan Steinhoff for usefuldiscussions. We also thank the anonymous referee for ahelpful suggestion. J. V. R. is supported by Fundaçãopara a Ciência e Tecnologia (FCT)-Portugal throughContract No. SFRH/BPD/47332/2008. R. S. is supportedby Grant No. 2012/20039-6, São Paulo ResearchFoundation (FAPESP). R. S. also thanks CentroMultidisciplinar de Astrofísica and Instituto SuperiorTécnico (IST) for hospitality during the initial phase ofthis work.

APPENDIX A: GAUGE TRANSFORMATIONS

It is convenient to decompose the metric perturbationinto scalars, vectors, and tensors according to their trans-formation properties under a general transformation of theangular coordinates fψ ; θ;ϕg. Thus, we have four scalarcomponents hAB, two vectors hAi, and one tensor hij, whereA, B ¼ t, r and i, j ¼ ψ , θ, ϕ. Each of these sectors can beexpanded in terms of Wigner functions DJ

KMðψ ; θ;ϕÞ; seereference [31]. In five dimensions there exist two commut-ing angular momentum operators whose Casimir operatorscoincide. The Wigner functions are the eigenfunctions ofthese operators.Given the high degree of symmetry of the matter

distribution we are assuming, namely Uð1Þ × SUð2Þ,the induced metric perturbation will preserve the symmetryof the background. This implies that only the zero-mode (J ¼ M ¼ K ¼ 0) of the expansion in Wignerfunctions can be excited and these modes decouple fromthe rest.According to [31], there are only seven independent

components in the perturbation zero-mode,

fhtt; htr; hrr; htψ ; hrψ ; hψψ ; hθθg; (A1)

while the four components hμθ with μ ≠ θ vanish identi-cally and the remaining components are given by

htϕ ¼ cos θ2

htψ ; hrϕ ¼ cos θ2

hrψ ;

hψϕ ¼ cos θ2

hψψ ; hϕϕ ¼ sin2θhθθ þcos2θ4

hψψ : (A2)

Under an infinitesimal coordinate transformation, themetric perturbation transforms as

hμν⟶hnewμν ¼ hμν þ∇ðμξνÞ: (A3)

In order not to spoil the symmetries of the background,we will consider only gauge transformations of the formξμ ¼ ðξt; ξr; ξψ ; 0; cos θ2 ξψÞ with ξt;r;ψ being functions of tand r only. By choosing

ξt ¼−f2

2rΩ

�hrψ þ

�1−

2r2ðf2−Ω2h2Þh2f2

�ξψrþ ∂rξψ

2

�;

ξr ¼−Z �

2htrþ2

rξtþ ∂rξt− 2

ðl2þ 2r2Þrl2f2

ðξtþΩξψ Þ�dr;

ξψ ¼−ðr2þ r−2ÞZ

r

1

Jðt; ~rÞð~r2 − ~r−2Þ8~r

d~r

þðr2− r−2ÞZ

r

1

Jðt; ~rÞð~r2þ ~r−2Þ8~r

d~r; (A4)

with

Jðt; rÞ ¼ 8r3Ωf2

�htr þΩhrψ −

2g2

r∂thθθ

�

−8r3 − 2rh2

h2hrψ − 2r2∂rhrψ ; (A5)

we manage to eliminate the components htr, hrψ , hrϕ andhθθ, thus bringing the metric perturbation to the form (28).The gauge fixing we have just performed still

leaves some residual gauge freedom: one can stillmake a coordinate transformation defined by ξresμ ¼ðζt; 0; ζψ ; 0; cos θ2 ζψ Þ, with

ζtðt; rÞ ¼ ω1ðtÞr2 þ ω2ðtÞr−2; ζψðt; rÞ

¼ −a�1þ r2

l2

�ω1ðtÞ þ

r4 þ l2r2 − 2Ml2

2aMl2r2ω2ðtÞ:(A6)

This leaves all the components unaltered except for htt andhtψ , which transform as

htt → htt − a

�1þ r2

l2

�ω01ðtÞ þ

r4 þ l2r2 − 2Ml2

2aMl2r2ω02ðtÞ;

htψ → htψ þ r2

2ω01ðtÞ þ

1

2r2ω02ðtÞ: (A7)

Several of the equations between (A4) and (A7) breakdown in the nonrotating limit, where a ¼ 0. This case mustbe dealt with separately, but it is naturally simpler.Assuming spherical symmetry of the background and ofthe perturbation, the only nonvanishing components of hμνare fhtt; htr; hrr; hψψ ; hψϕ; hθθ; hϕϕg. However, the latterthree components are determined by hψψ :

ROCHA, SANTARELLI, AND DELSATE PHYSICAL REVIEW D 89, 104006 (2014)

104006-10

hψϕ ¼cosθ2

hψψ ; hθθ ¼hψψ4

; hϕϕ¼hψψ4

: (A8)

By making a gauge transformation of the formξμ ¼ ðξt; ξr; 0; 0; 0Þ, with ξt;r given by

ξt ¼r4 þ l2r2 − 2Ml2

r2

×Z �

l2r3∂thψψðr4 þ l2r2 − 2Ml2Þ2 −

2rhtrr4 þ l2r2 − 2Ml2

�dr;

ξr ¼ −l2rhψψ

r4 þ l2r2 − 2Ml2; (A9)

we can eliminate htr and hψψ and thus in the nonrotatingcase we can gauge fix the metric perturbation to take theform

hμν ¼ diagfhttðt; rÞ; hrrðt; rÞ; 0; 0; 0g: (A10)

There is still some residual gauge freedom left. Namely,by performing a coordinate transformation defined byξresμ ¼ ðr4þl2r2−2Ml2

r2 ω0ðtÞ; 0; 0; 0; 0Þ, with ω0ðtÞ being a

generic function of time, the frrg component remainsunaltered while the fttg component changes as

htt → htt þr4 þ l2r2 − 2Ml2

r2ω00ðtÞ: (A11)

This exhausts the amount of gauge freedom initially presentin the metric perturbation tensor.

APPENDIX B: EQUATIONS GOVERNINGLINEAR PERTURBATIONS IN THE

ROTATING CASE

The spherically symmetric case a ¼ Lψ ¼ 0 is a veryspecial particular case in which one can solve the pertur-bation equations exactly. In this appendix we consider themore general case a ≠ 0, Lψ ≠ 0.Plugging the metric perturbation ansatz into the linear-

ized Einstein equations, one finds that seven of theseequations are automatically satisfied, leaving 8 nontrivialequations. Upon partial integration, the full system reducesto just four independent equations. Specifically, we get adecoupled PDE for the component hψψ ,

3l2ðr4 þ 2a2MÞ2r6 þ l2r4 þ 2Mða2 − l2Þr2 þ 2a2Ml2

∂2t hψψ −

3ðr4 þ 2a2MÞðr6 þ l2r4 þ 2Mða2 − l2Þr2 þ 2a2Ml2Þl2r4

∂2rhψψ

−3ðr4 þ 2a2MÞð3r10 − 3l2r8 þ 18l2Mr6 − 16a2l2Mr4 þ 20a2M2ða2 − l2Þr2 þ 12a4l2M2Þ

l2r5ð3r4 þ 2a2MÞ ∂rhψψ

þ 12ðr4 þ 2a2MÞð3r8 þ 6l2r6 þ 2Mð2a2 þ 3l2Þr4 þ 20a2l2Mr2 − 4a2M2ða2 − l2ÞÞl2r4ð3r4 þ 2a2MÞ hψψ

þ 3072πm0aMðr4 þ 2a2MÞð2aE − 3Lψ Þr2ð3r4 þ 2a2MÞ Θðr − RÞ þ 64πm0ðr4 þ 2a2MÞ

l2r7χ1ðt; rÞδðr − RÞ ¼ 0; (B1)

a coupled ODE for htψ and hψψ , which can be suggestively expressed as

∂r

�1

r3∂rðr2htψÞ

�¼ 1

r3ðr4 þ 2a2MÞð3r4 þ 2a2MÞðr6 þ l2r4 þ 2Mða2 − l2Þr2 þ 2a2Ml2Þ

×

�2aMr2ðr4 − 2a2MÞðr6 þ l2r4 þ 2Mða2 − l2Þr2 þ 2a2Ml2Þ∂2

rhψψ

−2aMr

ð3r4 þ 2a2MÞ ½−3r14 þ 9l2r12 þ 14Mða2 − 3l2Þr10 þ 46a2Ml2r8

− 4a2M2ð5a2 − 6l2Þr6 − 4a4M2l2r4 þ 8a4M3ða2 − l2Þr2 þ 8a6M3l2�∂rhψψ

−8aM

ð3r4 þ 2a2MÞ ½3r14 þ 9l2r12 − 6Mða2 − 3l2Þr10 þ 26a2Ml2r8

− 4a2M2ð7a2 − 6l2Þr6 − 20a4M2l2r4 − 8a4M3ða2 − l2Þr2 − 8a6M3l2�hψψ

−4096πm0a2M2l2ð2aE − 3Lψ Þr8

ð3r4 þ 2a2MÞ Θðr − RÞ þ 64πm0r3

3χ2ðt; rÞδðr − RÞ

�; (B2)

and two constraint equations determining hrr and htt,

COLLAPSING ROTATING SHELLS IN MYERS-PERRY-ADS … PHYSICAL REVIEW D 89, 104006 (2014)

104006-11

hrr ¼r6þl2r4þ 2Mða2−l2Þr2þ 2a2Ml2

l2rð3r4þ 2a2MÞ ∂rhψψ −2r6þl2r4 − 2a2Ml2

l2r2ð3r4þ 2a2MÞ hψψ þ64πm0ðEr4þ 2aMðaE−Lψ ÞÞ

r2ð3r4þ 2a2MÞ Θðr−RÞ;

(B3)

htt ¼ −r6 þ l2r4 þ 2Mða2 − l2Þr2 þ 2a2Ml2

2l2rð3r4 þ 2a2MÞ ∂rhψψ −2r6 þ l2r4 þ 2a2Mðr2 þ l2Þ

l2r2ð3r4 þ 2a2MÞ hψψ

−r6 þ l2r4 þ 2Mða2 − l2Þr2 þ 2a2Ml2

4aMl2r∂rhtψ þ r6 þ l2r4 − 2Mða2 þ l2Þr2 − 2a2Ml2

2aMl2r2htψ

þ 16πm0ð4aMl2Er2 þ Lψ ½3r6 þ 3l2r4 þ 2Mða2 − 3l2Þr2 þ 2a2Ml2�ÞaMl2ð3r4 þ 2a2MÞ Θðr − RÞ; (B4)

where R ¼ RðtÞ is to be understood as a function of t, and for convenience we have introduced in Eqs. (B1) and (B2) thefollowing functions multiplying the delta distributions:

χ1ðt; rÞ≡ −4a2Ml2Er2 þ Lψ

�6aMl2r2 − r2ð3r4 þ 2a2MÞ ðR

4 þ l2R2 − 2Ml2ÞLψ þ 2aMl2E

ER4 þ 2aMðaE − LψÞ�

þ 4a2Ml6r6ðER4 þ 2aMðaE − LψÞÞR0ðtÞ2ðr6 þ l2r4 þ 2Mða2 − l2Þr2 þ 2a2Ml2ÞðR6 þ l2R4 þ 2Mða2 − l2ÞR2 þ 2a2Ml2Þ ; (B5)

χ2ðt; rÞ≡ 4aMl2Er2ð3r4 þ 10a2MÞ þ 4aMl4r6ð3r4 þ 2a2MÞr6 þ l2r4 þ 2Mða2 − l2Þr2 þ 2a2Ml2

R0ðtÞ2 _TðτÞ

þ Lψ ½3ð3r10 þ 3l2r8 þ ð8a2M − 6l2MÞr6 þ 8a2Ml2r4 þ 4a2M2ða2 − 5l2Þr2 þ 4a4M2l2Þþ 4aMl2r2ð3r4 þ 2a2MÞΨ0ðtÞ�: (B6)

In writing these equations we have dropped a couple ofintegration constants. This is justified since we are lookingfor perturbations that are sourced by the test shell. Thus, theprocedure is to (i) find a solution of the PDE for thecomponent hψψ , (ii) replace it in the coupled ODE anddetermine the solution for htψ , and (iii) obtain componentshrr and htt from the constraints (B3) and (B4).

APPENDIX C: STRATEGY TO SOLVE PDEsWITH DISTRIBUTIONAL SOURCES

The equation (B1) is a second order nonhomogeneousPDE, with source terms proportional to distributions,namely the Heaviside function and the Dirac δ-function.It is convenient to recast the problem as a homogeneousPDE with prescribed boundary conditions dictated by thenonhomogeneous terms. This can be done as follows.Plugging in solutions of the form (35), the differential

equation will take the general form

SðRðtÞ; rÞΘðr − RðtÞÞ þ PðRðtÞ; rÞδðr − RðtÞÞþQðRðtÞ; rÞδ0ðr − RðtÞÞ ¼ 0: (C1)

One concludes immediately that the coefficient of theHeaviside function must vanish since it is the only termwith support away from r ¼ RðtÞ. By integrating in r or inR, we obtain three other constraints that may be regarded asboundary conditions. The final result is

SðR; rÞ ¼ 0; (C2)

QðR;RÞ ¼ 0; (C3)

PðR;RÞ − ∂rQðR;RÞ ¼ 0; (C4)

PðR;RÞ þ ∂RQðR;RÞ ¼ 0: (C5)

In fact, assuming Q to be an analytic function in thevariable r, Eq. (C5) can be derived from Eqs. (C3) and(C4), so it need not be imposed separately.

ROCHA, SANTARELLI, AND DELSATE PHYSICAL REVIEW D 89, 104006 (2014)

104006-12

[1] R. P. Kerr, Phys. Rev. Lett. 11, 237 (1963).[2] B. F. Whiting, J. Math. Phys. (N.Y.) 30, 1301 (1989).[3] T. Nakamura, Prog. Theor. Phys. 65, 1876 (1981).[4] R. F. Stark and T. Piran, Phys. Rev. Lett. 55, 891 (1985); 56,

97 (1986).[5] R. V. Wagoner, Phys. Rev. 138, B1583 (1965).[6] P. S. Joshi and D. Malafarina, Int. J. Mod. Phys. D 20, 2641

(2011).[7] J. M. Cohen, Phys. Rev. 173, 1258 (1968).[8] L. Lindblom and D. R. Brill, Phys. Rev. D 10, 3151 (1974).[9] R. B. Mann, J. J. Oh, and M.-I. Park, Phys. Rev. D 79,

064005 (2009).[10] J. V. Rocha and V. Cardoso, Phys. Rev. D 83, 104037

(2011).[11] To be precise, the number of independent angular momenta

is equal to the rank of the rotation group, which is incorrespondence with the number of orthogonal rotationplanes.

[12] H. K. Kunduri, J. Lucietti, and H. S. Reall, Phys. Rev. D 74,084021 (2006).

[13] P. Bizon, T. Chmaj, and B. G. Schmidt, Phys. Rev. Lett. 95,071102 (2005).

[14] F. J. Zerilli, Phys. Rev. D 2, 2141 (1970).[15] R. Penrose, Riv. Nuovo Cimento 1, 252 (1969); R. Penrose,

Gen. Relativ. Gravit. 34, 1141 (2002).[16] R. Wald, Ann. Phys. (N.Y.) 82, 548 (1974).[17] M. Bouhmadi-López, V. Cardoso, A. Nerozzi, and J. V.

Rocha, Phys. Rev. D 81, 084051 (2010).[18] Y. Zhang and S. Gao, Int. J. Mod. Phys. D 23, 1450044

(2014).[19] J. V. Rocha and R. Santarelli, Phys. Rev. D 89, 064065

(2014).[20] O. Aharony, S. S. Gubser, J. M. Maldacena, H. Ooguri, and

Y. Oz, Phys. Rep. 323, 183 (2000).

[21] S. Bhattacharyya and S. Minwalla, J. High Energy Phys. 09(2009) 034.

[22] D. Garfinkle and L. A. Pando Zayas, Phys. Rev. D 84,066006 (2011).

[23] H. Bantilan, F. Pretorius, and S. S. Gubser, Phys. Rev. D 85,084038 (2012).

[24] V. Balasubramanian and P. Kraus, Commun. Math. Phys.208, 413 (1999).

[25] S. W. Hawking, C. J. Hunter, and M.M. Taylor-Robinson,Phys. Rev. D 59, 064005 (1999).

[26] G.W. Gibbons, H. Lu, D. N. Page, and C. N. Pope, Phys.Rev. Lett. 93, 171102 (2004).

[27] G.W. Gibbons, H. Lu, D. N. Page, and C. N. Pope, J. Geom.Phys. 53, 49 (2005).

[28] R. C. Myers and M. J. Perry, Ann. Phys. (N.Y.) 172, 304(1986).

[29] For equal angular momenta, this symmetry is enhancedfrom Uð1Þ2 to Uð2Þ.

[30] T. Ortín, Gravity and Strings (Cambridge University Press,Cambridge, England, 2004).

[31] K. Murata, Prog. Theor. Phys. 121, 1099 (2009).[32] C. O. Lousto and R. H. Price, Phys. Rev. D 55, 2124

(1997).[33] T. Delsate, J. V. Rocha, and R. Santarelli (to be published).[34] The restriction to equally spinning backgrounds was in-

strumental in rendering the linearized perturbation equationsamenable to analytic treatment. Relaxing this assumption,one generically obtains additional independent metric per-turbation components, a larger set of equations to solve, andexplicit dependence on polar angles. Nevertheless, thegeneral approach we have followed is still applicable inthese cases.

[35] P. Bizon and B. G. Schmidt, Int. J. Mod. Phys. D 15, 2217(2006).

COLLAPSING ROTATING SHELLS IN MYERS-PERRY-ADS … PHYSICAL REVIEW D 89, 104006 (2014)

104006-13