Independência Regra de Bayes Redes...

• Independência

• Regra de Bayes

• Redes Bayesianas

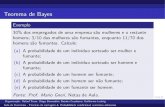
Inferência Probabilística

• Evidência observada: dor. Qual é a probabilidade de cárie dado que foi observado dor?

𝑃 𝑐á𝑟𝑖𝑒 𝑑𝑜𝑟 =𝑃(𝑐á𝑟𝑖𝑒 ∧ 𝑑𝑜𝑟)

𝑃(𝑑𝑜𝑟= 0,6

Independência

• E se for adicionando uma quarta variável, Tempo?

• A distribuição conjunta total então se torna P(DorDeDente, Boticão, Cárie, Tempo), que tem 2 × 2 × 2 × 4 = 32 entradas.

• Assim, contém quatro “edições” da tabela

P(DorDeDente, Boticão, Cárie), uma para cada estado do tempo (ensolarado, chuva, nublado, neve).

Independência

• Mas, P(dordedente, boticão, cárie, nublado) e P(dordedente, boticão, cárie) estão relacionadas?

Pela regra do produto: 𝑃(𝑑𝑜𝑟𝑑𝑒𝑑𝑒𝑛𝑡𝑒, 𝑏𝑜𝑡𝑖𝑐ã𝑜, 𝑐á𝑟𝑖𝑒, 𝑛𝑢𝑏𝑙𝑎𝑑𝑜)= 𝑃 𝑛𝑢𝑏𝑙𝑎𝑑𝑜 𝑑𝑜𝑟𝑑𝑒𝑑𝑒𝑛𝑡𝑒, 𝑏𝑜𝑡𝑖𝑐ã𝑜, 𝑐á𝑟𝑖𝑒) 𝑃(𝑑𝑜𝑟𝑑𝑒𝑑𝑒𝑛𝑡𝑒, 𝑏𝑜𝑡𝑖𝑐ã𝑜, 𝑐á𝑟𝑖𝑒 • Mas, variáveis dentárias não têm influência no tempo e,

portanto, tem-se:

𝑃 𝑛𝑢𝑏𝑙𝑎𝑑𝑜 𝑑𝑜𝑟𝑑𝑒𝑑𝑒𝑛𝑡𝑒, 𝑏𝑜𝑡𝑖𝑐ã𝑜, 𝑐á𝑟𝑖𝑒) = 𝑃(𝑛𝑢𝑏𝑙𝑎𝑑𝑜)

• Consequentemente:

𝑃(𝑑𝑜𝑟𝑑𝑒𝑑𝑒𝑛𝑡𝑒, 𝑏𝑜𝑡𝑖𝑐ã𝑜, 𝑐á𝑟𝑖𝑒, 𝑛𝑢𝑏𝑙𝑎𝑑𝑜)= 𝑃(𝑛𝑢𝑏𝑙𝑎𝑑𝑜) 𝑃(𝑑𝑜𝑟𝑑𝑒𝑑𝑒𝑛𝑡𝑒, 𝑏𝑜𝑡𝑖𝑐ã𝑜, 𝑐á𝑟𝑖𝑒

Independência

• A propriedade

𝑃 𝑛𝑢𝑏𝑙𝑎𝑑𝑜 𝑑𝑜𝑟𝑑𝑒𝑑𝑒𝑛𝑡𝑒, 𝑏𝑜𝑡𝑖𝑐ã𝑜, 𝑐á𝑟𝑖𝑒) = 𝑃(𝑛𝑢𝑏𝑙𝑎𝑑𝑜) é chamada independência (também independência marginal e independência absoluta). A independência entre as proposições 𝑎 e 𝑏 pode ser escrita como:

𝑃 𝑎 𝑏 = 𝑃 𝑎 ou

𝑃 𝑏 𝑎 = 𝑃 𝑏 ou

𝑃 𝑎 ∧ 𝑏 = 𝑃 𝑎 𝑃 𝑏

Independência • A definição geral de independência condicional de duas

variáveis 𝑋, 𝑌, dada uma terceira variável 𝑍 é:

𝑃 𝑋, 𝑌 𝑍 = 𝑃 𝑋 𝑍 𝑃(𝑌|𝑍

As formas equivalentes

𝑃 𝑎 𝑏 = 𝑃 𝑎 ou 𝑃 𝑏 𝑎 = 𝑃 𝑏

São:

𝑃 𝑋 𝑌, 𝑍 = 𝑃 𝑋|𝑍 ou 𝑃 𝑌 𝑋, 𝑍 = 𝑃 𝑌|𝑍

Isso quer dizer que se o objetivo é saber a probabilidade de 𝑋, então tanto faz o valor de 𝑌 se você já sabe o valor de 𝑍. • Exemplo: Trovão é condicionalmente independente de

Chuva, dado Relâmpago

P(Trovão/ Chuva, Relâmpago) = P(Trovão/ Relâmpago)

Independência

• A tabela de 32 elementos para quatro variáveis pode ser construída a partir de uma tabela de oito elementos e uma tabela de quatro elementos.

23 x 4 =32

23 = 8 4

23 + 4 < 32

Regra de Bayes

• A regra do produto:

𝑃 𝑎 ∧ 𝑏 = 𝑃 𝑎 𝑏)𝑃(𝑏) ou 𝑃 𝑎 ∧ 𝑏 = 𝑃 𝑏 𝑎)𝑃(𝑎)

• Igualando os dois membros obtém-se a Regra de Bayes:

𝑃 𝑏 | 𝑎 =𝑃 𝑎 𝑏)𝑃(𝑏)

𝑃(𝑎)

Regra de Bayes

• A Regra de Bayes também é conhecida como Lei de Bayes ou

Teorema de Bayes. • Em IA é a base para inferência probabilística.

• Interpretação da Regra de Bayes:

𝑃 𝑐𝑎𝑢𝑠𝑎 | 𝑒𝑓𝑒𝑖𝑡𝑜 =𝑃 𝑒𝑓𝑒𝑖𝑡𝑜 𝑐𝑎𝑢𝑠𝑎)𝑃(𝑐𝑎𝑢𝑠𝑎)

𝑃(𝑒𝑓𝑒𝑖𝑡𝑜)

Regra de Bayes 𝑃 𝐴 = 𝑃 𝐴 𝜔1 𝑃 𝜔1 + ⋯ 𝑃 𝐴 𝜔𝑛 𝑃 𝜔𝑛

n

i

ii

jj

j

PAP

PAPAP

1

)(*)|(

)(*)|()|(

𝑃(𝜔𝑗|𝐴) É a probabilidade de que a hipótese 𝜔𝑗 seja verdadeira, dada a evidência 𝐴.

Probabilidade de Bayes.

𝑃(𝐴|𝜔𝑗) É a probabilidade de que será observada a evidência 𝐴, dado que a hipótese 𝜔𝑗 é verdadeira.

𝑃(𝜔𝑗) É a Probabilidade “a priori” de que a hipótese 𝑗 seja verdadeira na ausência de quaisquer outra evidência

𝑃 𝐴 é a Probabilidade Total

𝑃 𝜔𝑗 | 𝐴 =𝑟𝑎𝑐𝑖𝑜𝑐í𝑛𝑖𝑜 𝑖𝑛𝑣𝑒𝑟𝑠𝑜

𝑃𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑑𝑎𝑑𝑒 𝑇𝑜𝑡𝑎𝑙

Regra de Bayes

• Exemplo: um médico sabe que a meningite faz o paciente ter uma rigidez no pescoço, digamos, durante 70% do tempo. O médico também conhece alguns fatos incondicionais: a probabilidade a priori de um paciente ter meningite é 1/50.000, e a probabilidade a priori de qualquer paciente ter rigidez no pescoço é 1%. Sendo s a proposição de que o paciente tem rigidez no pescoço e m a proposição de que o paciente tem meningite, temos:

Regra de Bayes

• Como pode-se obter 𝑃 𝑠 ¬ 𝑚 𝑃(¬ 𝑚 ?

• Sabemos que:

𝑃 𝑀 𝑠) = 𝛼[𝑃 𝑠 𝑚 𝑃(𝑚 + 𝑃 𝑠 ¬ 𝑚 𝑃(¬𝑚 ] 𝑃 𝑀 𝑠) = 𝛼 < 0,000014 , 0,09986 > 𝑃 𝑀 𝑠) = < 0,0014 , 0,9986 >

Regra de Bayes

• A forma geral da Regra de Bayes com normalização é:

𝑃 𝑌 𝑋) = 𝛼𝑃 𝑋 𝑌 𝑃(𝑌

• A Regra de Bayes , caso mais geral de variáveis multivaloradas:

𝑃 𝑌 | 𝑋 =𝑃 𝑋 𝑌)𝑃(𝑌)

𝑃(𝑋)

Regra de Bayes • Em geral, dada uma evidência prévia 𝑋 e alguma nova observação

(evidência prática) 𝒆, precisa-se calcular:

𝑃 𝑌 |𝑋, 𝒆 = 𝑃 𝑌 𝒆)𝑃 𝑋 𝑌, 𝒆)

𝑃 𝑋 𝒆)

• O tamanho do grupo de probabilidades conjuntas necessárias para

calcular esta função cresce 2n para n proposições.

• A distribuição de probabilidade conjunta pode se tornar intratavelmente grande.

• Independência e independência condicional entre variáveis pode reduzir o número de probabilidades que precisam ser especificadas (distribuição conjunta total).

• Redes bayesianas podem representar essencialmente qualquer distribuição de probabilidade conjunta completa e, em muitos casos, muito concisamente.

Redes Bayesianas

• Rede bayesiana (RB) é um grafo acíclico dirigido em que:

1. Cada nó representa a uma V.A., que pode ser discreta ou

contínua. 2. Um conjunto de ligações ou arcos dirigidos conectam

pares de nós 3. Cada nó recebe arcos dos nós que tem influencia direta

sobre ele. 4. Cada nó possui uma tabela de probabilidade condicional

associada que quantifica os efeitos que os pais têm sobre ele.

• A RB é composta por: Estrutura gráfica e Parâmetros

numéricos.

Redes Bayesianas

• A topologia da rede (o conjunto de nós e vínculos) especifica os relacionamentos de independência condicional válidos no domínio.

• O significado intuitivo de um arco é que X tem influência direta sobre Y: as causas devem ser pais dos efeitos.

Causa

Efeitos

Redes Bayesianas • Após da topologia da rede bayesiana ser definida, precisa-se

especificar uma distribuição de probabilidade condicional para cada variável, dados seus pais. • Relacionamentos das

variáveis Alarme, Terremoto, Roubo, JoãoLiga, MariaLiga

• As distribuições condicionais são mostradas como uma tabela de probabilidade condicional (TPC). Cada linha da TPC contém a probabilidade condicional de cada valor do nó para um caso de condicionamento. Um caso de condicionamento é apenas uma combinação possível de valores para os nós pai — uma miniatura do mundo possível.

Redes Bayesianas - Semântica

• Uma entrada genérica na distribuição conjunta é a probabilidade de uma conjunção de atribuições específicas a cada variável tal como 𝑃(𝑋1 = 𝑥1 ∧... ∧ 𝑋𝑛 = 𝑥𝑛), usa-se 𝑃(𝑥1, … 𝑥𝑛) de forma abreviada. O valor dessa entrada esta dado por:

Onde 𝑝𝑎𝑖𝑠 (𝑋𝑖) denota os valores em 𝑃𝑎𝑖𝑠 (𝑋𝑖)que aparecem em 𝑥1, 𝑥2, … 𝑥𝑛.

• Assim, cada entrada na distribuição conjunta é representada pelo produto dos elementos apropriados das TPC na rede bayesiana.

n

i

iin XpaisxxxP1

1 ))(/(),,(

Redes Bayesianas - Semântica

• É provado que os parâmetros 𝜃(𝑋𝑖|𝑃𝑎𝑖𝑠(𝑋𝑖)) são exatamente as probabilidade condicionais 𝑃(𝑋𝑖|𝑃𝑎𝑖𝑠(𝑋𝑖)) deduzidas pela distribuição conjunta. Assim reescreve-se a equação como: Isto é, as tabelas que chamamos de tabelas de probabilidade condicional realmente são tabelas de probabilidade condicional.

• E é essa equação que define o que significa uma rede

bayesiana.

n

i

iin XpaisxPxxP1

1 ))(/(),,(

Redes Bayesianas – Exemplo Alarme

Redes Bayesianas – Exemplo Alarme

• Cálculo da probabilidade conjunta:

• Calcular a probabilidade do evento que o alarme toca mas não houve assalto nem terremoto e que João e Maria telefonaram: P(J M A ~R ~T)

= P(J|A) P(M|A) P(A|~R ~T )P(~R)P(~T) = 0.9 x 0.7 x 0.001 x 0.999 x 0.998 = 0.00062 ou 0.062 %

n

i

iin XpaisxPxxP1

1 ))(/(),,(

Redes Bayesianas- Construção • A equação

• Implica certos relacionamentos de independência condicional, que podem ser usados na construção da topologia da rede: 1. Escreve-se as entradas na distribuição conjunta em termos de

probabilidade condicional usando a regra do produto:

n

i

iin XpaisxPxxP1

1 ))(/(),,(

Redes Bayesianas- Construção 2. A seguir, repete-se o processo reduzindo cada probabilidade

conjuntiva a uma probabilidade condicional e uma conjunção menor:

𝑃(𝑥1, …, 𝑥𝑛) = 𝑃 𝑥𝑛 𝑥𝑛−1, … 𝑥1 𝑃 𝑥𝑛−1 𝑥𝑛−2, … 𝑥1 … 𝑃 𝑥2 𝑥1 𝑃(𝑥1)

– Essa identidade é chamada de regra da cadeia.

– É válida para qualquer conjunto de variáveis aleatórias.

n

i

in xxxPxxP1

1111 ),.../(),,(

Redes Bayesianas- Construção

• Comparando:

• Com:

Vê-se que, a especificação da distribuição conjunta é equivalente à afirmação geral de que, para toda variável 𝑋𝑖 na rede, tem-se:

𝑃(𝑋𝑖|𝑋𝑖−1, … 𝑋1) = 𝑃(𝑋𝑖|𝑃𝑎𝑖𝑠(𝑋𝑖))

desde que 𝑃𝑎𝑖𝑠(𝑋𝑖) ⊆ {𝑋𝑖−1, …, 𝑋1}

• Esta última condição é satisfeita enumerando os nós em qualquer ordem consistente com a ordem parcial implícita na estrutura do grafo.

n

i

iin XpaisxPxxP1

1 ))(/(),,(

n

i

in xxxPxxP1

1111 ),.../(),,(

Redes Bayesianas- Construção • Para satisfazer a condição deve-se:

1. Nós: Primeiro determine o conjunto de variáveis que são necessárias para modelar o domínio. Agora as ordene, {X1, …, Xn}. Qualquer ordem vai funcionar, mas a rede resultante será mais compacta se as variáveis forem ordenadas de tal forma que as causas precedam os efeitos.

2. Vínculos: Para i = 1 até n faça: • Escolha, de X1,…, Xi-1, um conjunto mínimo de pais para Xi, tal que

a Equação 1 seja satisfeita.

• Para cada pai insira um vínculo do pai para Xi.

• TPCs: escreva a tabela de probabilidade condicional, P(Xi | Pais (Xi)).

Redes Bayesianas- Construção

Vejamos:

• Intuitivamente, os pais do nó Xi devem conter todos os nós em X1, …, Xi –1 que influenciam diretamente Xi.

• No caso do Alarme, vamos supor que completamos a rede , exceto pela escolha de pais para MariaLiga.

• MariaLiga certamente é influenciada pelo fato de haver ou não um Roubo ou um Terremoto, mas não é diretamente influenciada.

Redes Bayesianas- Construção • Intuitivamente, nosso conhecimento do domínio nos diz que

esses eventos influenciam a disposição de Maria para telefonar somente por seu efeito sobre o alarme.

• Além disso, dado o estado do alarme, o fato de João ligar não tem influência sobre a ligação de Maria.

• Em termos formais, acreditamos que a declaração de independência condicional a seguir seja válida:

P(MariaLiga | JoãoLiga, Alarme, Terremoto, Roubo) = P(MariaLiga |

Alarme).

• Assim, Alarme será o único nó pai para MariaLiga.

Redes Bayesianas- Construção • Como cada nó só é ligado aos nós anteriores, esse método de

construção garante que a rede é acíclica.

• Outra propriedade importante da rede bayesiana é que ela não contém valores de probabilidade redundante.

• Se não houver redundância, não há chance para inconsistência: é impossível para o engenheiro de conhecimento ou especialista de domínio criar uma rede bayesiana que viole os axiomas da probabilidade.

Independência Regra de Bayes Redes...

Documents

Transcript of Independência Regra de Bayes Redes...