UNIVERSIDADE FEDERAL FLUMINENSE

IME - Instituto de Matemática e Estatística

LANTE – Laboratório de Novas Tecnologias de Ensino

TRABALHO FINAL DA DISCIPLINA HMAP – 2010/4 NOME: Mário César Cunha

PÓLO: Botucatu- SP

GRUPO: 06

RESOLUÇÃO DA EQUACAO DO 2o GRAU PELOS MÉTODOS DE

AL-KHWARIZMI

Para exemplificar seus dois métodos, buscaremos a solução da equação do 2º grau

x² + 10x = 39. Esta equação é realmente encontrada no trabalho de Al-Khwarizmi.

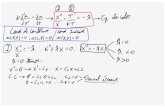
Solução da equação x² + 10x = 39 pelo 1º método de Al-Khwarizmi

Primeiramente, a equação é escrita na forma 394

1042 =⋅⋅+ xx ; ou seja,

392

542 =⋅⋅+ xx

Figura 1- Problema 1º método de Al- Khwarizmi

Figura 1. Na parte superior, a equação 392

542 =⋅⋅+ xx e interpretada geometricamente.

Na parte inferior, é completado o quadrado e resultando na equação equivalente

222

2

5439

2

54

2

54

⋅+=

⋅+⋅⋅+ xx

Interpretando geometricamente o lado esquerdo desta equação, como na figura 1, temos a

soma das áreas de um quadrado de lado x e de quatro retângulos de lados 5/2 e x

totalizando 39 unidades de área.

Completando entao essa soma de áreas com a área de quatro quadrados de lados 5/2, cada

um de área 25/4, obtém-se a área de um quadrado de lado 52

52 +=

⋅+ xx medindo então

6425394

25439 =+=

⋅+ unidades de área. Algebricamente,

222

2

5439

2

54

2

54

⋅+=

⋅+⋅⋅+ xx

ou seja,

( ) 6425395 2 =+=+x

de onde, então, Al-Khwarizmi deduz que

8645 ==+x

Chega-se então à solução x = 8 -5 = 3. Para Al-Khwarizmi porém, quantidades

negativas careciam de sentido. No seu método, a solução x = -8 -5 = -13 não vem à tona.

Ao resolvermos equações do 2º grau nos podemos, no entanto, usar o método geométrico

de Al-Khwarizmi para completar os quadrados e, ao final, “esquecê-lo”, deduzindo também

eventuais soluções negativas da equação.

Solução da equação x² + 10x = 39 pelo 2º método de Al-Khwarizmi

Neste método mais simples, a equação é escrita na forma x² + 5x + 5x = 39

Figura 2- Problema 2º método de Al- Khwarizmi

Figura 2. Na parte superior, a equacao x²+5x = 39 é interpretada geometricamente. Na parte

inferior, completando o quadrado resulta na equação equivalente

x² + 5x + 5x + 5² = 39+5²

Interpretando geometricamente o lado esquerdo desta equação, como na figura 2,

temos agora a soma das áreas de um quadrado de lado x e de dois retângulos de lados 5 e x

totalizando 39 unidades de área. Completando então essa soma de áreas com a área de um

quadrado de lado 5, portanto de área 25, obtém-se a área de um quadrado de lado x + 5,

medindo então 39 + 25 = 64 unidades de área. Algebricamente,

x² + 5x + 5x + 5² = 39+5²

de onde, então,

(x + 5)² = 39+25 = 64

de onde, então, Al-Khwarizmi deduz que

8645 ==+x

OBSERVAÇÃO: Mas e se tivermos que tratar da equação x² - 5x = 33? Como

interpretar geometricamente o completamento de quadrados, se agora estamos subtraindo

dois retângulos de lados 5 e x?

O melhor, neste caso, é fazer uma substituição x = -u, de onde x² = u². A equação

então se torna u²+8u = 33. Aplicando então o método geométrico de Al-Khwarizmi,

chegaremos às soluções u1 = 3 e u2 = -11, de onde obtemos x1 = -3 e x2 = 11.

Problemas complementares

1. (Al-Khwarizmi) Encontre o lado de um quadrado inscrito num triângulo de lados 10, 10

e 12. Resposta: O quadrado tem lado de comprimento 4,8.

2. (Al-Khwarizmi) Resolva as seguintes equa»c~oes :

(a) 50 + x² = 29+10x. Resposta: x1 = 7; x2 = 3.

(b) x² = 40x - 4x². Resposta: x1 = 8; x2 = 0

3. Resolva as seguintes equações

(a) x² - 16x + 80 = 0. Resposta: A equação não tem solução (real).

(b) x² - 12x = 28. Resposta: x1 = 14; x2 = -2