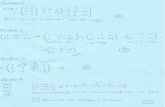Álgebra Linear
-
Upload
hugonunes89 -
Category
Documents
-
view
238 -
download
0
description
Transcript of Álgebra Linear

Álgebra LinearResolução da Prova
Prof. Me. Hugo Santos Nunes
Instituto Federal de Alagoas - IFAL
2015
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 1 / 12

Sejam: A =
1 2 3
2 1 −1
, B =
−2 0 1
3 0 1
, C =
−1
2
4
, D =[2 −1
], E =
1 0
3 −1
4 2
, F =
1 0
0 1
. Calcule, quando possível:
a) A · C =
1 2 3
2 1 −1
·−1
2
4
= 1 · (−1) + 2 · 2 + 3 · 4
2 · (−1) + 1 · 2 + (−1) · 4
=15−4
.
b) C ·A =
−1
2
4
·1 2 3
2 1 −1
. Não é possível.
c) C ·D+2E−At. =
−2 1
4 −2
8 −4
+2 0
6 −2
8 4
−1 2
2 1
3 −1
=0 1
10 −4
16 0
−1 2
2 1
3 −1
=−1 −1
8 −5
13 1
.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 2 / 12

Sejam: A =
1 2 3
2 1 −1
, B =
−2 0 1
3 0 1
, C =
−1
2
4
, D =[2 −1
], E =
1 0
3 −1
4 2
, F =
1 0
0 1
. Calcule, quando possível:
a) A · C =
1 2 3
2 1 −1
·−1
2
4
=
1 · (−1) + 2 · 2 + 3 · 4
2 · (−1) + 1 · 2 + (−1) · 4
=15−4
.
b) C ·A =
−1
2
4
·1 2 3
2 1 −1
. Não é possível.
c) C ·D+2E−At. =
−2 1
4 −2
8 −4
+2 0
6 −2
8 4
−1 2
2 1
3 −1
=0 1
10 −4
16 0
−1 2
2 1
3 −1
=−1 −1
8 −5
13 1
.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 2 / 12

Sejam: A =
1 2 3
2 1 −1
, B =
−2 0 1
3 0 1
, C =
−1
2
4
, D =[2 −1
], E =
1 0
3 −1
4 2
, F =
1 0
0 1
. Calcule, quando possível:
a) A · C =
1 2 3
2 1 −1
·−1
2
4
= 1 · (−1) + 2 · 2 + 3 · 4
2 · (−1) + 1 · 2 + (−1) · 4
=
15−4
.
b) C ·A =
−1
2
4
·1 2 3
2 1 −1
. Não é possível.
c) C ·D+2E−At. =
−2 1
4 −2
8 −4
+2 0
6 −2
8 4
−1 2
2 1
3 −1
=0 1
10 −4
16 0
−1 2
2 1
3 −1
=−1 −1
8 −5
13 1
.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 2 / 12

Sejam: A =
1 2 3
2 1 −1
, B =
−2 0 1
3 0 1
, C =
−1
2
4
, D =[2 −1
], E =
1 0
3 −1
4 2
, F =
1 0
0 1
. Calcule, quando possível:
a) A · C =
1 2 3
2 1 −1
·−1
2
4
= 1 · (−1) + 2 · 2 + 3 · 4
2 · (−1) + 1 · 2 + (−1) · 4
=15−4
.
b) C ·A =
−1
2
4
·1 2 3
2 1 −1
. Não é possível.
c) C ·D+2E−At. =
−2 1
4 −2
8 −4
+2 0
6 −2
8 4
−1 2
2 1
3 −1
=0 1
10 −4
16 0
−1 2
2 1
3 −1
=−1 −1
8 −5
13 1
.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 2 / 12

Sejam: A =
1 2 3
2 1 −1
, B =
−2 0 1
3 0 1
, C =
−1
2
4
, D =[2 −1
], E =
1 0
3 −1
4 2
, F =
1 0
0 1
. Calcule, quando possível:
a) A · C =
1 2 3
2 1 −1
·−1
2
4
= 1 · (−1) + 2 · 2 + 3 · 4
2 · (−1) + 1 · 2 + (−1) · 4
=15−4
.
b) C ·A =
−1
2
4
·1 2 3
2 1 −1
.
Não é possível.
c) C ·D+2E−At. =
−2 1
4 −2
8 −4
+2 0
6 −2
8 4
−1 2
2 1
3 −1
=0 1
10 −4
16 0
−1 2
2 1
3 −1
=−1 −1
8 −5
13 1
.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 2 / 12

Sejam: A =
1 2 3
2 1 −1
, B =
−2 0 1
3 0 1
, C =
−1
2
4
, D =[2 −1
], E =
1 0
3 −1
4 2
, F =
1 0
0 1
. Calcule, quando possível:
a) A · C =
1 2 3
2 1 −1
·−1
2
4
= 1 · (−1) + 2 · 2 + 3 · 4
2 · (−1) + 1 · 2 + (−1) · 4
=15−4
.
b) C ·A =
−1
2
4
·1 2 3
2 1 −1
. Não é possível.
c) C ·D+2E−At. =
−2 1
4 −2
8 −4
+2 0
6 −2
8 4
−1 2
2 1
3 −1
=0 1
10 −4
16 0
−1 2
2 1
3 −1
=−1 −1
8 −5
13 1
.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 2 / 12

Sejam: A =
1 2 3
2 1 −1
, B =
−2 0 1
3 0 1
, C =
−1
2
4
, D =[2 −1
], E =
1 0
3 −1
4 2
, F =
1 0
0 1
. Calcule, quando possível:
a) A · C =
1 2 3
2 1 −1
·−1
2
4
= 1 · (−1) + 2 · 2 + 3 · 4
2 · (−1) + 1 · 2 + (−1) · 4
=15−4
.
b) C ·A =
−1
2
4
·1 2 3
2 1 −1
. Não é possível.
c) C ·D+2E−At.
=
−2 1
4 −2
8 −4
+2 0
6 −2
8 4
−1 2
2 1
3 −1
=0 1
10 −4
16 0
−1 2
2 1
3 −1
=−1 −1
8 −5
13 1
.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 2 / 12

Sejam: A =
1 2 3
2 1 −1
, B =
−2 0 1
3 0 1
, C =
−1
2
4
, D =[2 −1
], E =
1 0
3 −1
4 2
, F =
1 0
0 1
. Calcule, quando possível:
a) A · C =
1 2 3
2 1 −1
·−1
2
4
= 1 · (−1) + 2 · 2 + 3 · 4
2 · (−1) + 1 · 2 + (−1) · 4
=15−4
.
b) C ·A =
−1
2
4
·1 2 3
2 1 −1
. Não é possível.
c) C ·D+2E−At. =
−2 1
4 −2
8 −4
+
2 0
6 −2
8 4
−1 2
2 1
3 −1
=0 1
10 −4
16 0
−1 2
2 1
3 −1
=−1 −1
8 −5
13 1
.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 2 / 12

Sejam: A =
1 2 3
2 1 −1
, B =
−2 0 1
3 0 1
, C =
−1
2
4
, D =[2 −1
], E =
1 0
3 −1
4 2
, F =
1 0
0 1
. Calcule, quando possível:
a) A · C =
1 2 3
2 1 −1
·−1
2
4
= 1 · (−1) + 2 · 2 + 3 · 4
2 · (−1) + 1 · 2 + (−1) · 4
=15−4
.
b) C ·A =
−1
2
4
·1 2 3
2 1 −1
. Não é possível.
c) C ·D+2E−At. =
−2 1
4 −2
8 −4
+2 0
6 −2
8 4
−
1 2
2 1
3 −1
=0 1
10 −4
16 0
−1 2
2 1
3 −1
=−1 −1
8 −5
13 1
.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 2 / 12

Sejam: A =
1 2 3
2 1 −1
, B =
−2 0 1
3 0 1
, C =
−1
2
4
, D =[2 −1
], E =
1 0
3 −1
4 2
, F =
1 0
0 1
. Calcule, quando possível:
a) A · C =
1 2 3
2 1 −1
·−1
2
4
= 1 · (−1) + 2 · 2 + 3 · 4
2 · (−1) + 1 · 2 + (−1) · 4
=15−4
.
b) C ·A =
−1
2
4
·1 2 3
2 1 −1
. Não é possível.
c) C ·D+2E−At. =
−2 1
4 −2
8 −4
+2 0
6 −2
8 4
−1 2
2 1
3 −1
=
0 1
10 −4
16 0
−1 2
2 1
3 −1
=−1 −1
8 −5
13 1
.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 2 / 12

Sejam: A =
1 2 3
2 1 −1
, B =
−2 0 1
3 0 1
, C =
−1
2
4
, D =[2 −1
], E =
1 0
3 −1
4 2
, F =
1 0
0 1
. Calcule, quando possível:
a) A · C =
1 2 3
2 1 −1
·−1
2
4
= 1 · (−1) + 2 · 2 + 3 · 4
2 · (−1) + 1 · 2 + (−1) · 4
=15−4
.
b) C ·A =
−1
2
4
·1 2 3
2 1 −1
. Não é possível.
c) C ·D+2E−At. =
−2 1
4 −2
8 −4
+2 0
6 −2
8 4
−1 2
2 1
3 −1
=0 1
10 −4
16 0
−1 2
2 1
3 −1
=
−1 −1
8 −5
13 1
.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 2 / 12

Sejam: A =
1 2 3
2 1 −1
, B =
−2 0 1
3 0 1
, C =
−1
2
4
, D =[2 −1
], E =
1 0
3 −1
4 2
, F =
1 0
0 1
. Calcule, quando possível:
a) A · C =
1 2 3
2 1 −1
·−1
2
4
= 1 · (−1) + 2 · 2 + 3 · 4
2 · (−1) + 1 · 2 + (−1) · 4
=15−4
.
b) C ·A =
−1
2
4
·1 2 3
2 1 −1
. Não é possível.
c) C ·D+2E−At. =
−2 1
4 −2
8 −4
+2 0
6 −2
8 4
−1 2
2 1
3 −1
=0 1
10 −4
16 0
−1 2
2 1
3 −1
=−1 −1
8 −5
13 1
.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 2 / 12

d) Ct · E − 3D.
Ct =[−1 2 4
], Ct · E =
[21 6
]e − 3D =
[−6 3
].
[21 6
]+[−6 3
]=[15 9
].
e) E · F +At −Bt 1 0
3 −1
4 2
+
1 2
2 1
3 −1
−−2 3
0 0
1 1
=
4 −1
5 0
6 0
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 3 / 12

d) Ct · E − 3D.
Ct =[−1 2 4
],
Ct · E =[21 6
]e − 3D =
[−6 3
].
[21 6
]+[−6 3
]=[15 9
].
e) E · F +At −Bt 1 0
3 −1
4 2
+
1 2
2 1
3 −1
−−2 3
0 0
1 1
=
4 −1
5 0
6 0
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 3 / 12

d) Ct · E − 3D.
Ct =[−1 2 4
], Ct · E =
[21 6
]
e − 3D =[−6 3
].
[21 6
]+[−6 3
]=[15 9
].
e) E · F +At −Bt 1 0
3 −1
4 2
+
1 2
2 1
3 −1
−−2 3
0 0
1 1
=
4 −1
5 0
6 0
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 3 / 12

d) Ct · E − 3D.
Ct =[−1 2 4
], Ct · E =
[21 6
]e − 3D =
[−6 3
].
[21 6
]+[−6 3
]=[15 9
].
e) E · F +At −Bt 1 0
3 −1
4 2
+
1 2
2 1
3 −1
−−2 3
0 0
1 1
=
4 −1
5 0
6 0
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 3 / 12

d) Ct · E − 3D.
Ct =[−1 2 4
], Ct · E =
[21 6
]e − 3D =
[−6 3
].
[21 6
]+[−6 3
]
=[15 9
].
e) E · F +At −Bt 1 0
3 −1
4 2
+
1 2
2 1
3 −1
−−2 3
0 0
1 1
=
4 −1
5 0
6 0
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 3 / 12

d) Ct · E − 3D.
Ct =[−1 2 4
], Ct · E =
[21 6
]e − 3D =
[−6 3
].
[21 6
]+[−6 3
]=[15 9
].
e) E · F +At −Bt
1 0
3 −1
4 2
+
1 2
2 1
3 −1
−−2 3
0 0
1 1
=
4 −1
5 0
6 0
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 3 / 12

d) Ct · E − 3D.
Ct =[−1 2 4
], Ct · E =
[21 6
]e − 3D =
[−6 3
].
[21 6
]+[−6 3
]=[15 9
].
e) E · F +At −Bt 1 0
3 −1
4 2
+
1 2
2 1
3 −1
−−2 3
0 0
1 1
=
4 −1
5 0
6 0
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 3 / 12

d) Ct · E − 3D.
Ct =[−1 2 4
], Ct · E =
[21 6
]e − 3D =
[−6 3
].
[21 6
]+[−6 3
]=[15 9
].
e) E · F +At −Bt 1 0
3 −1
4 2
+
1 2
2 1
3 −1
−
−2 3
0 0
1 1
=
4 −1
5 0
6 0
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 3 / 12

d) Ct · E − 3D.
Ct =[−1 2 4
], Ct · E =
[21 6
]e − 3D =
[−6 3
].
[21 6
]+[−6 3
]=[15 9
].
e) E · F +At −Bt 1 0
3 −1
4 2
+
1 2
2 1
3 −1
−−2 3
0 0
1 1
=
4 −1
5 0
6 0
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 3 / 12

d) Ct · E − 3D.
Ct =[−1 2 4
], Ct · E =
[21 6
]e − 3D =
[−6 3
].
[21 6
]+[−6 3
]=[15 9
].
e) E · F +At −Bt 1 0
3 −1
4 2
+
1 2
2 1
3 −1
−−2 3
0 0
1 1
=
4 −1
5 0
6 0
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 3 / 12

Questão: Calcule os determinantes usando a Regra de Sarrus.Lembrete: se detA 6= 0 então a matriz A é inversível. Quando necessário, determine x de modoque a matriz seja inversível.
a) A =
1 0 2
2 x 1
1 3 0
Solução: Devemos ter det 6= 0. Assim:
1 0 2
2 x 1
1 3 0
6= 0⇒
1 0 2
... 1 0
2 x 1... 2 x
1 3 0... 1 3
6= 0
(1 · x · 0) + (0 · 1 · 1) + (2 · 2 · 3)− (2 · x · 1)− (1 · 1 · 3)− (0 · 2 · 0) 6= 0
0 + 0 + 12− 2x− 3− 0 6= 0
9− 2x 6= 0
2x 6= 9
x 6=9
2
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 4 / 12

Questão: Calcule os determinantes usando a Regra de Sarrus.Lembrete: se detA 6= 0 então a matriz A é inversível. Quando necessário, determine x de modoque a matriz seja inversível.
a) A =
1 0 2
2 x 1
1 3 0
Solução: Devemos ter det 6= 0. Assim:
1 0 2
2 x 1
1 3 0
6= 0⇒
1 0 2
... 1 0
2 x 1... 2 x
1 3 0... 1 3
6= 0
(1 · x · 0) + (0 · 1 · 1) + (2 · 2 · 3)− (2 · x · 1)− (1 · 1 · 3)− (0 · 2 · 0) 6= 0
0 + 0 + 12− 2x− 3− 0 6= 0
9− 2x 6= 0
2x 6= 9
x 6=9
2
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 4 / 12

Questão: Calcule os determinantes usando a Regra de Sarrus.Lembrete: se detA 6= 0 então a matriz A é inversível. Quando necessário, determine x de modoque a matriz seja inversível.
a) A =
1 0 2
2 x 1
1 3 0
Solução: Devemos ter det 6= 0.
Assim:
1 0 2
2 x 1
1 3 0
6= 0⇒
1 0 2
... 1 0
2 x 1... 2 x
1 3 0... 1 3
6= 0
(1 · x · 0) + (0 · 1 · 1) + (2 · 2 · 3)− (2 · x · 1)− (1 · 1 · 3)− (0 · 2 · 0) 6= 0
0 + 0 + 12− 2x− 3− 0 6= 0
9− 2x 6= 0
2x 6= 9
x 6=9
2
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 4 / 12

Questão: Calcule os determinantes usando a Regra de Sarrus.Lembrete: se detA 6= 0 então a matriz A é inversível. Quando necessário, determine x de modoque a matriz seja inversível.
a) A =
1 0 2
2 x 1
1 3 0
Solução: Devemos ter det 6= 0. Assim:
1 0 2
2 x 1
1 3 0
6= 0
⇒
1 0 2
... 1 0
2 x 1... 2 x
1 3 0... 1 3
6= 0
(1 · x · 0) + (0 · 1 · 1) + (2 · 2 · 3)− (2 · x · 1)− (1 · 1 · 3)− (0 · 2 · 0) 6= 0
0 + 0 + 12− 2x− 3− 0 6= 0
9− 2x 6= 0
2x 6= 9
x 6=9
2
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 4 / 12

Questão: Calcule os determinantes usando a Regra de Sarrus.Lembrete: se detA 6= 0 então a matriz A é inversível. Quando necessário, determine x de modoque a matriz seja inversível.
a) A =
1 0 2
2 x 1
1 3 0
Solução: Devemos ter det 6= 0. Assim:
1 0 2
2 x 1
1 3 0
6= 0⇒
1 0 2
... 1 0
2 x 1... 2 x
1 3 0... 1 3
6= 0
(1 · x · 0) + (0 · 1 · 1) + (2 · 2 · 3)− (2 · x · 1)− (1 · 1 · 3)− (0 · 2 · 0) 6= 0
0 + 0 + 12− 2x− 3− 0 6= 0
9− 2x 6= 0
2x 6= 9
x 6=9
2
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 4 / 12

Questão: Calcule os determinantes usando a Regra de Sarrus.Lembrete: se detA 6= 0 então a matriz A é inversível. Quando necessário, determine x de modoque a matriz seja inversível.
a) A =
1 0 2
2 x 1
1 3 0
Solução: Devemos ter det 6= 0. Assim:
1 0 2
2 x 1
1 3 0
6= 0⇒
1 0 2
... 1 0
2 x 1... 2 x
1 3 0... 1 3
6= 0
(1 · x · 0) + (0 · 1 · 1) + (2 · 2 · 3)− (2 · x · 1)− (1 · 1 · 3)− (0 · 2 · 0) 6= 0
0 + 0 + 12− 2x− 3− 0 6= 0
9− 2x 6= 0
2x 6= 9
x 6=9
2
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 4 / 12

Questão: Calcule os determinantes usando a Regra de Sarrus.Lembrete: se detA 6= 0 então a matriz A é inversível. Quando necessário, determine x de modoque a matriz seja inversível.
a) A =
1 0 2
2 x 1
1 3 0
Solução: Devemos ter det 6= 0. Assim:
1 0 2
2 x 1
1 3 0
6= 0⇒
1 0 2
... 1 0
2 x 1... 2 x
1 3 0... 1 3
6= 0
(1 · x · 0) + (0 · 1 · 1) + (2 · 2 · 3)− (2 · x · 1)− (1 · 1 · 3)− (0 · 2 · 0) 6= 0
0 + 0 + 12− 2x− 3− 0 6= 0
9− 2x 6= 0
2x 6= 9
x 6=9
2
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 4 / 12

Questão: Calcule os determinantes usando a Regra de Sarrus.Lembrete: se detA 6= 0 então a matriz A é inversível. Quando necessário, determine x de modoque a matriz seja inversível.
a) A =
1 0 2
2 x 1
1 3 0
Solução: Devemos ter det 6= 0. Assim:
1 0 2
2 x 1
1 3 0
6= 0⇒
1 0 2
... 1 0
2 x 1... 2 x
1 3 0... 1 3
6= 0
(1 · x · 0) + (0 · 1 · 1) + (2 · 2 · 3)− (2 · x · 1)− (1 · 1 · 3)− (0 · 2 · 0) 6= 0
0 + 0 + 12− 2x− 3− 0 6= 0
9− 2x 6= 0
2x 6= 9
x 6=9
2
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 4 / 12

Questão: Calcule os determinantes usando a Regra de Sarrus.Lembrete: se detA 6= 0 então a matriz A é inversível. Quando necessário, determine x de modoque a matriz seja inversível.
a) A =
1 0 2
2 x 1
1 3 0
Solução: Devemos ter det 6= 0. Assim:
1 0 2
2 x 1
1 3 0
6= 0⇒
1 0 2
... 1 0
2 x 1... 2 x
1 3 0... 1 3
6= 0
(1 · x · 0) + (0 · 1 · 1) + (2 · 2 · 3)− (2 · x · 1)− (1 · 1 · 3)− (0 · 2 · 0) 6= 0
0 + 0 + 12− 2x− 3− 0 6= 0
9− 2x 6= 0
2x 6= 9
x 6=9
2
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 4 / 12

Questão: Calcule os determinantes usando a Regra de Sarrus.Lembrete: se detA 6= 0 então a matriz A é inversível. Quando necessário, determine x de modoque a matriz seja inversível.
a) A =
1 0 2
2 x 1
1 3 0
Solução: Devemos ter det 6= 0. Assim:
1 0 2
2 x 1
1 3 0
6= 0⇒
1 0 2
... 1 0
2 x 1... 2 x
1 3 0... 1 3
6= 0
(1 · x · 0) + (0 · 1 · 1) + (2 · 2 · 3)− (2 · x · 1)− (1 · 1 · 3)− (0 · 2 · 0) 6= 0
0 + 0 + 12− 2x− 3− 0 6= 0
9− 2x 6= 0
2x 6= 9
x 6=9
2
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 4 / 12

b) B =
1 2 3
4 5 6
7 8 9
.
Solução: detB =
1 2 3
... 1 2
4 5 6... 4 5
7 8 9... 7 8
detB = (1 · 5 · 9) + (2 · 6 · 7) + (3 · 4 · 8)− (3 · 5 · 7)− (1 · 6 · 8)− (2 · 4 · 9)detB = 45 + 84 + 96− 105− 48− 72
detB = 0
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 5 / 12

b) B =
1 2 3
4 5 6
7 8 9
.
Solução: detB =
1 2 3
... 1 2
4 5 6... 4 5
7 8 9... 7 8
detB = (1 · 5 · 9) + (2 · 6 · 7) + (3 · 4 · 8)− (3 · 5 · 7)− (1 · 6 · 8)− (2 · 4 · 9)detB = 45 + 84 + 96− 105− 48− 72
detB = 0
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 5 / 12

b) B =
1 2 3
4 5 6
7 8 9
.
Solução: detB =
1 2 3
... 1 2
4 5 6... 4 5
7 8 9... 7 8
detB = (1 · 5 · 9) + (2 · 6 · 7) + (3 · 4 · 8)− (3 · 5 · 7)− (1 · 6 · 8)− (2 · 4 · 9)
detB = 45 + 84 + 96− 105− 48− 72
detB = 0
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 5 / 12

b) B =
1 2 3
4 5 6
7 8 9
.
Solução: detB =
1 2 3
... 1 2
4 5 6... 4 5
7 8 9... 7 8
detB = (1 · 5 · 9) + (2 · 6 · 7) + (3 · 4 · 8)− (3 · 5 · 7)− (1 · 6 · 8)− (2 · 4 · 9)detB = 45 + 84 + 96− 105− 48− 72
detB = 0
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 5 / 12

b) B =
1 2 3
4 5 6
7 8 9
.
Solução: detB =
1 2 3
... 1 2
4 5 6... 4 5
7 8 9... 7 8
detB = (1 · 5 · 9) + (2 · 6 · 7) + (3 · 4 · 8)− (3 · 5 · 7)− (1 · 6 · 8)− (2 · 4 · 9)detB = 45 + 84 + 96− 105− 48− 72
detB = 0
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 5 / 12

Calcule os determinantes abaixo usando o Teorema de Laplace.
a)
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
2 0 −2 1
0 1 3 1
2 1 0 3
1 1 1 0
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣.
Solução: a)
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
2 0 −2 1
0 1 3 1
2 1 0 3
1 1 1 0
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣.
detA = 2 · (−1)1+1
∣∣∣∣∣∣∣∣∣1 3 1
1 0 3
1 1 0
∣∣∣∣∣∣∣∣∣+ 0 + (−2) · (−1)1+3
∣∣∣∣∣∣∣∣∣0 1 1
2 1 3
1 1 0
∣∣∣∣∣∣∣∣∣+ 1 · (−1)1+4
∣∣∣∣∣∣∣∣∣0 1 3
2 1 0
1 1 1
∣∣∣∣∣∣∣∣∣detA = 2(9 + 1− 3)− 2(3 + 2− 1)− 1(6− 3− 2)
detA = 5
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 6 / 12

Calcule os determinantes abaixo usando o Teorema de Laplace.
a)
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
2 0 −2 1
0 1 3 1
2 1 0 3
1 1 1 0
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣.
Solução: a)
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
2 0 −2 1
0 1 3 1
2 1 0 3
1 1 1 0
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣.
detA = 2 · (−1)1+1
∣∣∣∣∣∣∣∣∣1 3 1
1 0 3
1 1 0
∣∣∣∣∣∣∣∣∣+ 0 + (−2) · (−1)1+3
∣∣∣∣∣∣∣∣∣0 1 1
2 1 3
1 1 0
∣∣∣∣∣∣∣∣∣+ 1 · (−1)1+4
∣∣∣∣∣∣∣∣∣0 1 3
2 1 0
1 1 1
∣∣∣∣∣∣∣∣∣detA = 2(9 + 1− 3)− 2(3 + 2− 1)− 1(6− 3− 2)
detA = 5
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 6 / 12

Calcule os determinantes abaixo usando o Teorema de Laplace.
a)
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
2 0 −2 1
0 1 3 1
2 1 0 3
1 1 1 0
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣.
Solução: a)
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
2 0 −2 1
0 1 3 1
2 1 0 3
1 1 1 0
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣.
detA = 2 · (−1)1+1
∣∣∣∣∣∣∣∣∣1 3 1
1 0 3
1 1 0
∣∣∣∣∣∣∣∣∣+ 0 + (−2) · (−1)1+3
∣∣∣∣∣∣∣∣∣0 1 1
2 1 3
1 1 0
∣∣∣∣∣∣∣∣∣+ 1 · (−1)1+4
∣∣∣∣∣∣∣∣∣0 1 3
2 1 0
1 1 1
∣∣∣∣∣∣∣∣∣
detA = 2(9 + 1− 3)− 2(3 + 2− 1)− 1(6− 3− 2)
detA = 5
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 6 / 12

Calcule os determinantes abaixo usando o Teorema de Laplace.
a)
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
2 0 −2 1
0 1 3 1
2 1 0 3
1 1 1 0
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣.
Solução: a)
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
2 0 −2 1
0 1 3 1
2 1 0 3
1 1 1 0
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣.
detA = 2 · (−1)1+1
∣∣∣∣∣∣∣∣∣1 3 1
1 0 3
1 1 0
∣∣∣∣∣∣∣∣∣+ 0 + (−2) · (−1)1+3
∣∣∣∣∣∣∣∣∣0 1 1
2 1 3
1 1 0
∣∣∣∣∣∣∣∣∣+ 1 · (−1)1+4
∣∣∣∣∣∣∣∣∣0 1 3
2 1 0
1 1 1
∣∣∣∣∣∣∣∣∣detA = 2(9 + 1− 3)− 2(3 + 2− 1)− 1(6− 3− 2)
detA = 5
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 6 / 12

Calcule os determinantes abaixo usando o Teorema de Laplace.
a)
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
2 0 −2 1
0 1 3 1
2 1 0 3
1 1 1 0
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣.
Solução: a)
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
2 0 −2 1
0 1 3 1
2 1 0 3
1 1 1 0
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣.
detA = 2 · (−1)1+1
∣∣∣∣∣∣∣∣∣1 3 1
1 0 3
1 1 0
∣∣∣∣∣∣∣∣∣+ 0 + (−2) · (−1)1+3
∣∣∣∣∣∣∣∣∣0 1 1
2 1 3
1 1 0
∣∣∣∣∣∣∣∣∣+ 1 · (−1)1+4
∣∣∣∣∣∣∣∣∣0 1 3
2 1 0
1 1 1
∣∣∣∣∣∣∣∣∣detA = 2(9 + 1− 3)− 2(3 + 2− 1)− 1(6− 3− 2)
detA = 5
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 6 / 12

b)
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
1 2 1 0
2 0 1 1
3 0 1 2
1 1 0 1
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣.
Solução:
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
1 2 1 0
2 0 1 1
3 0 1 2
1 1 0 1
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣.
detB = 2 · (−1)1+2
∣∣∣∣∣∣∣∣∣2 1 1
3 1 2
1 0 1
∣∣∣∣∣∣∣∣∣+ 1 · (−1)4+2 ·
∣∣∣∣∣∣∣∣∣1 1 0
2 1 1
3 1 2
∣∣∣∣∣∣∣∣∣detB = 0
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 7 / 12

b)
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
1 2 1 0
2 0 1 1
3 0 1 2
1 1 0 1
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣.
Solução:
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
1 2 1 0
2 0 1 1
3 0 1 2
1 1 0 1
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣.
detB = 2 · (−1)1+2
∣∣∣∣∣∣∣∣∣2 1 1
3 1 2
1 0 1
∣∣∣∣∣∣∣∣∣+ 1 · (−1)4+2 ·
∣∣∣∣∣∣∣∣∣1 1 0
2 1 1
3 1 2
∣∣∣∣∣∣∣∣∣detB = 0
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 7 / 12

b)
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
1 2 1 0
2 0 1 1
3 0 1 2
1 1 0 1
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣.
Solução:
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
1 2 1 0
2 0 1 1
3 0 1 2
1 1 0 1
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣.
detB = 2 · (−1)1+2
∣∣∣∣∣∣∣∣∣2 1 1
3 1 2
1 0 1
∣∣∣∣∣∣∣∣∣+ 1 · (−1)4+2 ·
∣∣∣∣∣∣∣∣∣1 1 0
2 1 1
3 1 2
∣∣∣∣∣∣∣∣∣
detB = 0
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 7 / 12

b)
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
1 2 1 0
2 0 1 1
3 0 1 2
1 1 0 1
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣.
Solução:
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
1 2 1 0
2 0 1 1
3 0 1 2
1 1 0 1
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣.
detB = 2 · (−1)1+2
∣∣∣∣∣∣∣∣∣2 1 1
3 1 2
1 0 1
∣∣∣∣∣∣∣∣∣+ 1 · (−1)4+2 ·
∣∣∣∣∣∣∣∣∣1 1 0
2 1 1
3 1 2
∣∣∣∣∣∣∣∣∣detB = 0
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 7 / 12

Resolva os sistemas abaixo usando a Regra de Cramer.
a)
x + y = 1
−2x + 3y − 3z = 2
x + z = 1
Solução:
D =
∣∣∣∣∣∣∣∣∣1 1 0
−2 3 −3
1 0 1
∣∣∣∣∣∣∣∣∣ = 2, Dx =
∣∣∣∣∣∣∣∣∣1 1 0
2 3 −3
1 0 1
∣∣∣∣∣∣∣∣∣ = −2
Dy =
∣∣∣∣∣∣∣∣∣1 1 0
−2 2 −3
1 1 1
∣∣∣∣∣∣∣∣∣ = 4, Dz =
∣∣∣∣∣∣∣∣∣1 1 1
−2 3 2
1 0 1
∣∣∣∣∣∣∣∣∣ = 4
Logo:
x =Dx
D⇒−22
= −1, y =Dy
D⇒
4
2= 2, z =
Dz
D⇒
4
2= 2.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 8 / 12

Resolva os sistemas abaixo usando a Regra de Cramer.
a)
x + y = 1
−2x + 3y − 3z = 2
x + z = 1
Solução:
D =
∣∣∣∣∣∣∣∣∣1 1 0
−2 3 −3
1 0 1
∣∣∣∣∣∣∣∣∣ = 2, Dx =
∣∣∣∣∣∣∣∣∣1 1 0
2 3 −3
1 0 1
∣∣∣∣∣∣∣∣∣ = −2
Dy =
∣∣∣∣∣∣∣∣∣1 1 0
−2 2 −3
1 1 1
∣∣∣∣∣∣∣∣∣ = 4, Dz =
∣∣∣∣∣∣∣∣∣1 1 1
−2 3 2
1 0 1
∣∣∣∣∣∣∣∣∣ = 4
Logo:
x =Dx
D⇒−22
= −1, y =Dy
D⇒
4
2= 2, z =
Dz
D⇒
4
2= 2.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 8 / 12

Resolva os sistemas abaixo usando a Regra de Cramer.
a)
x + y = 1
−2x + 3y − 3z = 2
x + z = 1
Solução:
D =
∣∣∣∣∣∣∣∣∣1 1 0
−2 3 −3
1 0 1
∣∣∣∣∣∣∣∣∣ = 2, Dx =
∣∣∣∣∣∣∣∣∣1 1 0
2 3 −3
1 0 1
∣∣∣∣∣∣∣∣∣ = −2
Dy =
∣∣∣∣∣∣∣∣∣1 1 0
−2 2 −3
1 1 1
∣∣∣∣∣∣∣∣∣ = 4, Dz =
∣∣∣∣∣∣∣∣∣1 1 1
−2 3 2
1 0 1
∣∣∣∣∣∣∣∣∣ = 4
Logo:
x =Dx
D⇒−22
= −1, y =Dy
D⇒
4
2= 2, z =
Dz
D⇒
4
2= 2.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 8 / 12

Resolva os sistemas abaixo usando a Regra de Cramer.
a)
x + y = 1
−2x + 3y − 3z = 2
x + z = 1
Solução:
D =
∣∣∣∣∣∣∣∣∣1 1 0
−2 3 −3
1 0 1
∣∣∣∣∣∣∣∣∣ = 2, Dx =
∣∣∣∣∣∣∣∣∣1 1 0
2 3 −3
1 0 1
∣∣∣∣∣∣∣∣∣ = −2
Dy =
∣∣∣∣∣∣∣∣∣1 1 0
−2 2 −3
1 1 1
∣∣∣∣∣∣∣∣∣ = 4, Dz =
∣∣∣∣∣∣∣∣∣1 1 1
−2 3 2
1 0 1
∣∣∣∣∣∣∣∣∣ = 4
Logo:
x =Dx
D⇒−22
= −1,
y =Dy
D⇒
4
2= 2, z =
Dz
D⇒
4
2= 2.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 8 / 12

Resolva os sistemas abaixo usando a Regra de Cramer.
a)
x + y = 1
−2x + 3y − 3z = 2
x + z = 1
Solução:
D =
∣∣∣∣∣∣∣∣∣1 1 0
−2 3 −3
1 0 1
∣∣∣∣∣∣∣∣∣ = 2, Dx =
∣∣∣∣∣∣∣∣∣1 1 0
2 3 −3
1 0 1
∣∣∣∣∣∣∣∣∣ = −2
Dy =
∣∣∣∣∣∣∣∣∣1 1 0
−2 2 −3
1 1 1
∣∣∣∣∣∣∣∣∣ = 4, Dz =
∣∣∣∣∣∣∣∣∣1 1 1
−2 3 2
1 0 1
∣∣∣∣∣∣∣∣∣ = 4
Logo:
x =Dx
D⇒−22
= −1, y =Dy
D⇒
4
2= 2,
z =Dz
D⇒
4
2= 2.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 8 / 12

Resolva os sistemas abaixo usando a Regra de Cramer.
a)
x + y = 1
−2x + 3y − 3z = 2
x + z = 1
Solução:
D =
∣∣∣∣∣∣∣∣∣1 1 0
−2 3 −3
1 0 1
∣∣∣∣∣∣∣∣∣ = 2, Dx =
∣∣∣∣∣∣∣∣∣1 1 0
2 3 −3
1 0 1
∣∣∣∣∣∣∣∣∣ = −2
Dy =
∣∣∣∣∣∣∣∣∣1 1 0
−2 2 −3
1 1 1
∣∣∣∣∣∣∣∣∣ = 4, Dz =
∣∣∣∣∣∣∣∣∣1 1 1
−2 3 2
1 0 1
∣∣∣∣∣∣∣∣∣ = 4
Logo:
x =Dx
D⇒−22
= −1, y =Dy
D⇒
4
2= 2, z =
Dz
D⇒
4
2= 2.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 8 / 12

b)
2x + y + 3z = 0
2x − y − z = 0
x − 2y + 3z = 0
Solução:
D =
∣∣∣∣∣∣∣∣∣2 1 3
2 −1 −1
1 −2 3
∣∣∣∣∣∣∣∣∣ , Dx =
∣∣∣∣∣∣∣∣∣0 1 3
0 −1 −1
0 −2 3
∣∣∣∣∣∣∣∣∣
Dy =
∣∣∣∣∣∣∣∣∣2 0 3
2 0 −1
1 0 3
∣∣∣∣∣∣∣∣∣ , Dz =
∣∣∣∣∣∣∣∣∣2 1 0
2 −1 0
1 −2 0
∣∣∣∣∣∣∣∣∣Notem que temos Dx, Dy e Dz com colunas nulas. Logo, x = y = z = 0.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 9 / 12

b)
2x + y + 3z = 0
2x − y − z = 0
x − 2y + 3z = 0
Solução:
D =
∣∣∣∣∣∣∣∣∣2 1 3
2 −1 −1
1 −2 3
∣∣∣∣∣∣∣∣∣ , Dx =
∣∣∣∣∣∣∣∣∣0 1 3
0 −1 −1
0 −2 3
∣∣∣∣∣∣∣∣∣Dy =
∣∣∣∣∣∣∣∣∣2 0 3
2 0 −1
1 0 3
∣∣∣∣∣∣∣∣∣ , Dz =
∣∣∣∣∣∣∣∣∣2 1 0
2 −1 0
1 −2 0
∣∣∣∣∣∣∣∣∣Notem que temos Dx, Dy e Dz com colunas nulas. Logo, x = y = z = 0.
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 9 / 12

(Questão Extra.) Se A e B são matrizes inversíveis de mesma ordem, entãodet(A−1 ·B ·A)
detBé
igual a?
Pelo Teorema de Binet, propriedade 10 de determinantes, temos que: Se A e B são matrizesquadradas de orde n, então
det(A ·B) = detA · detB.
Assim:
det(A−1 ·B ·A)
detB=
detA−1 · detB · detAdetB
= detA−1 · detA
=1
detA· detA
= 1
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 10 / 12

(Questão Extra.) Se A e B são matrizes inversíveis de mesma ordem, entãodet(A−1 ·B ·A)
detBé
igual a?
Pelo Teorema de Binet, propriedade 10 de determinantes, temos que: Se A e B são matrizesquadradas de orde n, então
det(A ·B) = detA · detB.
Assim:
det(A−1 ·B ·A)
detB=
detA−1 · detB · detAdetB
= detA−1 · detA
=1
detA· detA
= 1
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 10 / 12

(Questão Extra.) Se A e B são matrizes inversíveis de mesma ordem, entãodet(A−1 ·B ·A)
detBé
igual a?
Pelo Teorema de Binet, propriedade 10 de determinantes, temos que: Se A e B são matrizesquadradas de orde n, então
det(A ·B) = detA · detB.
Assim:
det(A−1 ·B ·A)
detB
=detA−1 · detB · detA
detB
= detA−1 · detA
=1
detA· detA
= 1
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 10 / 12

(Questão Extra.) Se A e B são matrizes inversíveis de mesma ordem, entãodet(A−1 ·B ·A)
detBé
igual a?
Pelo Teorema de Binet, propriedade 10 de determinantes, temos que: Se A e B são matrizesquadradas de orde n, então
det(A ·B) = detA · detB.
Assim:
det(A−1 ·B ·A)
detB=
detA−1 · detB · detAdetB
= detA−1 · detA
=1
detA· detA
= 1
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 10 / 12

(Questão Extra.) Se A e B são matrizes inversíveis de mesma ordem, entãodet(A−1 ·B ·A)
detBé
igual a?
Pelo Teorema de Binet, propriedade 10 de determinantes, temos que: Se A e B são matrizesquadradas de orde n, então
det(A ·B) = detA · detB.
Assim:
det(A−1 ·B ·A)
detB=
detA−1 · detB · detAdetB
= detA−1 · detA
=1
detA· detA
= 1
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 10 / 12

(Questão Extra.) Se A e B são matrizes inversíveis de mesma ordem, entãodet(A−1 ·B ·A)
detBé
igual a?
Pelo Teorema de Binet, propriedade 10 de determinantes, temos que: Se A e B são matrizesquadradas de orde n, então
det(A ·B) = detA · detB.
Assim:
det(A−1 ·B ·A)
detB=
detA−1 · detB · detAdetB
= detA−1 · detA
=1
detA· detA
= 1
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 10 / 12

(Questão Extra.) Se A e B são matrizes inversíveis de mesma ordem, entãodet(A−1 ·B ·A)
detBé
igual a?
Pelo Teorema de Binet, propriedade 10 de determinantes, temos que: Se A e B são matrizesquadradas de orde n, então
det(A ·B) = detA · detB.
Assim:
det(A−1 ·B ·A)
detB=
detA−1 · detB · detAdetB
= detA−1 · detA
=1
detA· detA
= 1
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 10 / 12

Ache a matriz inversa de
A =
1 1 1
2 1 4
2 3 5
Solução: Usando o método de Gauss-Jordan:1 1 1 | 1 0 0
2 1 4 | 0 1 0
2 3 5 | 0 0 1
−2L1+L2−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
−2L1+L3−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
L2+L3−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
15L3−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 11 / 12

Ache a matriz inversa de
A =
1 1 1
2 1 4
2 3 5
Solução: Usando o método de Gauss-Jordan:
1 1 1 | 1 0 0
2 1 4 | 0 1 0
2 3 5 | 0 0 1
−2L1+L2−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
−2L1+L3−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
L2+L3−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
15L3−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 11 / 12

Ache a matriz inversa de
A =
1 1 1
2 1 4
2 3 5
Solução: Usando o método de Gauss-Jordan:
1 1 1 | 1 0 0
2 1 4 | 0 1 0
2 3 5 | 0 0 1
−2L1+L2−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
−2L1+L3−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
L2+L3−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
15L3−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 11 / 12

Ache a matriz inversa de
A =
1 1 1
2 1 4
2 3 5
Solução: Usando o método de Gauss-Jordan:
1 1 1 | 1 0 0
2 1 4 | 0 1 0
2 3 5 | 0 0 1
−2L1+L2−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
−2L1+L3−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
L2+L3−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
15L3−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 11 / 12

Ache a matriz inversa de
A =
1 1 1
2 1 4
2 3 5
Solução: Usando o método de Gauss-Jordan:
1 1 1 | 1 0 0
2 1 4 | 0 1 0
2 3 5 | 0 0 1
−2L1+L2−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
−2L1+L3−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
L2+L3−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
15L3−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 11 / 12

Ache a matriz inversa de
A =
1 1 1
2 1 4
2 3 5
Solução: Usando o método de Gauss-Jordan:
1 1 1 | 1 0 0
2 1 4 | 0 1 0
2 3 5 | 0 0 1
−2L1+L2−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
−2L1+L3−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
L2+L3−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
15L3−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 11 / 12

Ache a matriz inversa de
A =
1 1 1
2 1 4
2 3 5
Solução: Usando o método de Gauss-Jordan:
1 1 1 | 1 0 0
2 1 4 | 0 1 0
2 3 5 | 0 0 1
−2L1+L2−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
−2L1+L3−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
L2+L3−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
15L3−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 11 / 12

Ache a matriz inversa de
A =
1 1 1
2 1 4
2 3 5
Solução: Usando o método de Gauss-Jordan:
1 1 1 | 1 0 0
2 1 4 | 0 1 0
2 3 5 | 0 0 1
−2L1+L2−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
−2L1+L3−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
L2+L3−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
15L3−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 11 / 12

Ache a matriz inversa de
A =
1 1 1
2 1 4
2 3 5
Solução: Usando o método de Gauss-Jordan:
1 1 1 | 1 0 0
2 1 4 | 0 1 0
2 3 5 | 0 0 1
−2L1+L2−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
−2L1+L3−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
L2+L3−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
15L3−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 11 / 12

Ache a matriz inversa de
A =
1 1 1
2 1 4
2 3 5
Solução: Usando o método de Gauss-Jordan:
1 1 1 | 1 0 0
2 1 4 | 0 1 0
2 3 5 | 0 0 1
−2L1+L2−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
−2L1+L3−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
L2+L3−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
15L3−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 11 / 12

Ache a matriz inversa de
A =
1 1 1
2 1 4
2 3 5
Solução: Usando o método de Gauss-Jordan:
1 1 1 | 1 0 0
2 1 4 | 0 1 0
2 3 5 | 0 0 1
−2L1+L2−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
−2L1+L3−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
L2+L3−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
15L3−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 11 / 12

Ache a matriz inversa de
A =
1 1 1
2 1 4
2 3 5
Solução: Usando o método de Gauss-Jordan:
1 1 1 | 1 0 0
2 1 4 | 0 1 0
2 3 5 | 0 0 1
−2L1+L2−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
−2L1+L3−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
L2+L3−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
15L3−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 11 / 12

Ache a matriz inversa de
A =
1 1 1
2 1 4
2 3 5
Solução: Usando o método de Gauss-Jordan:
1 1 1 | 1 0 0
2 1 4 | 0 1 0
2 3 5 | 0 0 1
−2L1+L2−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
2 3 5 | 0 0 1
−2L1+L3−−−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 1 3 | −2 0 1
L2+L3−−−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 5 | −4 1 1
15L3−−−→
1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 11 / 12

1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
−L3+L1−−−−−−→
1 1 1 | 9
5− 1
5− 1
5
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
1 1 1 | 9
5− 1
5− 1
5
0 −1 0 | −2 1 0
0 0 1 | − 45
15
15
−2L3+L2−−−−−−−→
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
L2+L1−−−−−→
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
−L2−−−→
1 0 0 | 7
525
− 35
0 1 0 | 25
− 35
25
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 12 / 12

1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
−L3+L1−−−−−−→
1 1 1 | 9
5− 1
5− 1
5
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
1 1 1 | 9
5− 1
5− 1
5
0 −1 0 | −2 1 0
0 0 1 | − 45
15
15
−2L3+L2−−−−−−−→
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
L2+L1−−−−−→
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
−L2−−−→
1 0 0 | 7
525
− 35
0 1 0 | 25
− 35
25
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 12 / 12

1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
−L3+L1−−−−−−→
1 1 1 | 9
5− 1
5− 1
5
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
1 1 1 | 9
5− 1
5− 1
5
0 −1 0 | −2 1 0
0 0 1 | − 45
15
15
−2L3+L2−−−−−−−→
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
L2+L1−−−−−→
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
−L2−−−→
1 0 0 | 7
525
− 35
0 1 0 | 25
− 35
25
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 12 / 12

1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
−L3+L1−−−−−−→
1 1 1 | 9
5− 1
5− 1
5
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
1 1 1 | 9
5− 1
5− 1
5
0 −1 0 | −2 1 0
0 0 1 | − 45
15
15
−2L3+L2−−−−−−−→
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
L2+L1−−−−−→
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
−L2−−−→
1 0 0 | 7
525
− 35
0 1 0 | 25
− 35
25
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 12 / 12

1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
−L3+L1−−−−−−→
1 1 1 | 9
5− 1
5− 1
5
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
1 1 1 | 9
5− 1
5− 1
5
0 −1 0 | −2 1 0
0 0 1 | − 45
15
15
−2L3+L2−−−−−−−→
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
L2+L1−−−−−→
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
−L2−−−→
1 0 0 | 7
525
− 35
0 1 0 | 25
− 35
25
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 12 / 12

1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
−L3+L1−−−−−−→
1 1 1 | 9
5− 1
5− 1
5
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
1 1 1 | 9
5− 1
5− 1
5
0 −1 0 | −2 1 0
0 0 1 | − 45
15
15
−2L3+L2−−−−−−−→
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
L2+L1−−−−−→
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
−L2−−−→
1 0 0 | 7
525
− 35
0 1 0 | 25
− 35
25
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 12 / 12

1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
−L3+L1−−−−−−→
1 1 1 | 9
5− 1
5− 1
5
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
1 1 1 | 9
5− 1
5− 1
5
0 −1 0 | −2 1 0
0 0 1 | − 45
15
15
−2L3+L2−−−−−−−→
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
L2+L1−−−−−→
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
−L2−−−→
1 0 0 | 7
525
− 35
0 1 0 | 25
− 35
25
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 12 / 12

1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
−L3+L1−−−−−−→
1 1 1 | 9
5− 1
5− 1
5
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
1 1 1 | 9
5− 1
5− 1
5
0 −1 0 | −2 1 0
0 0 1 | − 45
15
15
−2L3+L2−−−−−−−→
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
L2+L1−−−−−→
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
−L2−−−→
1 0 0 | 7
525
− 35
0 1 0 | 25
− 35
25
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 12 / 12

1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
−L3+L1−−−−−−→
1 1 1 | 9
5− 1
5− 1
5
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
1 1 1 | 9
5− 1
5− 1
5
0 −1 0 | −2 1 0
0 0 1 | − 45
15
15
−2L3+L2−−−−−−−→
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
L2+L1−−−−−→
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
−L2−−−→
1 0 0 | 7
525
− 35
0 1 0 | 25
− 35
25
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 12 / 12

1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
−L3+L1−−−−−−→
1 1 1 | 9
5− 1
5− 1
5
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
1 1 1 | 9
5− 1
5− 1
5
0 −1 0 | −2 1 0
0 0 1 | − 45
15
15
−2L3+L2−−−−−−−→
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
L2+L1−−−−−→
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
−L2−−−→
1 0 0 | 7
525
− 35
0 1 0 | 25
− 35
25
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 12 / 12

1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
−L3+L1−−−−−−→
1 1 1 | 9
5− 1
5− 1
5
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
1 1 1 | 9
5− 1
5− 1
5
0 −1 0 | −2 1 0
0 0 1 | − 45
15
15
−2L3+L2−−−−−−−→
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
L2+L1−−−−−→
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
−L2−−−→
1 0 0 | 7
525
− 35
0 1 0 | 25
− 35
25
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 12 / 12

1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
−L3+L1−−−−−−→
1 1 1 | 9
5− 1
5− 1
5
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
1 1 1 | 9
5− 1
5− 1
5
0 −1 0 | −2 1 0
0 0 1 | − 45
15
15
−2L3+L2−−−−−−−→
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
L2+L1−−−−−→
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
−L2−−−→
1 0 0 | 7
525
− 35
0 1 0 | 25
− 35
25
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 12 / 12

1 1 1 | 1 0 0
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
−L3+L1−−−−−−→
1 1 1 | 9
5− 1
5− 1
5
0 −1 2 | −2 1 0
0 0 1 | − 45
15
15
1 1 1 | 9
5− 1
5− 1
5
0 −1 0 | −2 1 0
0 0 1 | − 45
15
15
−2L3+L2−−−−−−−→
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
1 1 0 | 9
5− 1
5− 1
5
0 −1 0 | − 25
35
− 25
0 0 1 | − 45
15
15
L2+L1−−−−−→
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
1 0 0 | 7
525− 3
5
0 −1 0 | − 25
35− 2
5
0 0 1 | − 45
15
15
−L2−−−→
1 0 0 | 7
525
− 35
0 1 0 | 25
− 35
25
0 0 1 | − 45
15
15
Prof. Me. Hugo Santos Nunes (Instituto Federal de Alagoas - IFAL) Álgebra Linear 2015 12 / 12