EDA - Árvores AVL_

Árvores AVL

Introdução

Um dos argumentos favoráveis ao uso de árvores éque o processo de busca na mesma é muito maisrápido do que em listas encadeadas.Mas, tal argumento nem sempre se mantém. Dependede como é a árvore.Observe as árvores da figura abaixo:

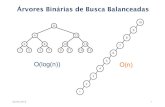
Todas elas armazenam os mesmos dados.Qual delas é a melhor? Qual é a pior?No pior caso, quantas comparações são necessáriaspara se encontrar um elemento na árvore (a)? E naárvore (c)?

Árvores Balanceadas

Dizemos que uma árvore está balanceada emaltura (ou em profundidade) quando, para cada nóda mesma, a diferença entre as alturas de suas duassubárvores é igual a -1, 0 ou 1.A esta diferença de altura damos o nome de fator debalanceamento.A figura abaixo mostra as árvores anteriores com aindicação em cada nó da diferença entre suas sub-árvores esquerda e direita.

28/10/2010 EDA - Árvores AVL

ucb.br/prg/professores/…/avl.html 1/6You created this PDF from an application that is not licensed to print to novaPDF printer (http://www.novapdf.com)

http://www.novapdf.com

Vantagem da Árvore BalanceadaAltura Nós em um nível Nós em todos os níveis

1 20 = 1 1 = 21 - 1

2 21 = 2 22 - 1 = 3

3 22 = 4 23 - 1 = 7

4 23 = 8 24 - 1 = 15

11 210 = 1024 211 - 1 = 2047

20 219 = 524288 220 - 1 = 1048575

h 2h - 1 2h - 1 = n

Com base na tabela acima, se tivéssemos 1.048.575elementos, poderíamos armazená-los em uma árvorebinária perfeitamente balanceada com 20 níveis.Em outras palavras, poderíamos localizar um elementoqualquer dentro dessa árvore com apenas 20comparações.

Árvores AVL

Quando da inserção ou remoção de algum elementode uma árvore balanceada, o balanceamento damesma pode ser afetado.Para fazer o rebalanceamento da árvore, existeminúmeras técnicas. Algumas delas, entretanto, usamalgoritmos que fazem o rebalanceamento global daárvore, exigindo assim que sejam utilizadas estruturasauxiliares para tal.Por outro lado, o rebalanceamento pode ser realizadolocalmente, caso apenas uma parte da árvore tenhasido afetada com a inserção ou remoção de umelemento.Em 1962, dois pesquisadores elaboraram um métodopara efetuar o rebalanceamento de uma árvore. Talárvore ficou conhecida como AVL (Adel'son-Vel'skii eLandis).

Inserindo elementos em uma Árvore AVL

Se o fator de balanceamento de um nó qualquer emuma árvore AVL se torna menor que -1 ou maior que1, então a árvore precisa ser balanceada.Vamos supor que um nó Y será inserido em umaárvore A (AVL) e provocará um desbalanceamento.Para mantermos a árvore A como AVL, é necessárioefetuar um rebalanceamento através de rotações noprimeiro ancestral de Y que teve o seu fator debalanceamento alterado para -2 ou +2.Considere X como sendo o ancestral afetado com ainclusão de Y.Para haver o desbalanceamento da árvore A, quatrosão as situações possíveis:

Y é inserido na sub-árvore direita do filho àdireita de X




Y é inserido na sub-árvore direita do filho àesquerda de X

Y é inserido na sub-árvore esqueda do filho àdireita de X




int fb; // fator de balanceamento struct no_AVL *pai; struct no_AVL *esq; struct no_AVL *dir;}typedef struct no_AVL AVL;

Implementando as rotações em uma ÁrvoreAVL

Rotação Esqueda

AVL *rotacao_esqueda(AVL *no) { AVL *temp; temp = no->dir; no->dir = temp->esq; if (temp->esq != NULL) temp->esq->pai = no; temp->esq = no; temp->pai = no->pai; no->pai->esq = temp; no->pai = temp; no->fb = 0; return temp;}

Rotação Direita

AVL *rotacao_direita(AVL *no) { AVL *temp; temp = no->esq; no->esq = temp->dir; if (temp->dir != NULL) temp->dir->pai = no; temp->dir = no; temp->pai = no->pai; no->pai->dir = temp; no->pai = temp; no->fb = 0; return temp;}

Rotação Esqueda Direita

AVL *rotacao_esqueda_direita(AVL *no) { AVL *pai; AVL *no_esq; AVL *novo_no; int fb_fdir;

pai = no->pai; no_esq = no->esq; fb_fdir = no_esq->dir->fb; no->esq = rotacao_esquerda(no_esq); novo_no = rotacao_direita(no); novo_no->pai = pai; no->fb = (fb_fdir == 1) ? -1 : 0; no_esq->fb = (fb_fdir == -1) ? 1 : 0; return novo_no;}

Rotação Direita Esqueda

AVL *rotacao_direita_esquerda(AVL *no) { AVL *pai;




novo_no = rotacao_esquerda(no); novo_no->pai = pai; no->fb = (fb_fesq == -1) ? 1 : 0; no_dir->fb = (fb_fesq == 1) ? -1 : 0; return novo_no;}

Implementando a inserção em uma Árvore AVL

Balanceamento à Esqueda

AVL *balanceamento_esquerda(AVL *no) { AVL *temp; temp = no->esq; if (temp->fb == 1) no = rotacao_direita(no); else no = rotacao_esquerda_direita(no); no->fb = 0; return no;}

Balanceamento à Direita

AVL *balanceamento_direita(AVL *no) { AVL *temp; temp = no->dir; if (temp->fb == -1) no = rotacao_esquerda(no); else no = rotacao_direita_esquerda(no); no->fb = 0; return no;}

Alocar memória para novo elemento da árvore

AVL *aloca_no(int info) { AVL *temp; temp = (AVL *) malloc(sizeof(AVL)); if (temp) { temp->info = info; temp->pai = NULL; temp->esq = NULL; temp->dir = NULL; temp->fb = 0; return temp; } return NULL;}

Inserção

AVL *insere(AVL *raiz, int info, bool *atualiza_fb) {

if (raiz == NULL) { AVL *temp = aloca_no(info); atualiza_fb = temp ? true : false; return temp; } else if (info < raiz->info) { raiz->esq = insere(raiz->esq, info, atualiza_fb); // Atualiza pai do nó inserido if (!raiz->esq->pai) { raiz->esq->pai = raiz; }




break; // Atualização do fb deve ser propagada. case 1: raiz = balanceamento_esquerda(raiz); // fb = 2 -> Balancear sub-árvore *atualiza_fb = false; // Não propagar a atualização do fb break; } } } else if (info > raiz->info) { raiz->dir = insere(raiz->dir, info, atualiza_fb); // Atualiza pai do nó inserido if (!raiz->dir->pai) { raiz->dir->pai = raiz; } if (*atualiza_fb) { switch (raiz->fb) { case 1: // Maior altura à esquerda e nó inserido à direita raiz->fb = 0; *atualiza_fb = false; // Não propagar a atualização do fb break; case 0: raiz->fb = -1; // Altura da direita maior que esquerda. break; // Atualização do fb deve ser propagada. case -1: raiz = balanceamento_direita(raiz); // fb = -22 -> Balancear sub-árvore *atualiza_fb = false; // Não propagar a atualização do fb break; } } } return raiz;}




EDA - Árvores AVL_

Documents

Transcript of EDA - Árvores AVL_