Universidade Estadual Paulista - Unesp · SE A acontecer e B ocorrer, ENTÃO faça-se C...

Universidade Estadual Paulista

“Júlio de Mesquita Filho” UNESP

Faculdade de Engenharia de Guaratinguetá

Departamento de Engenharia Elétrica

Estudo da influência dos erros da função de pertinência no controle lógico difuso

Autor: Fernando Setra Dantas Orientador: Prof. Dr. Galdenoro Botura Jr.

Maio de 2000

ÍNDICE

1. RESUMO DO PLANO INICIAL ........................................................................... 1

2. OBJETIVOS ............................................................................................................. 1

3. INTRODUÇÃO ........................................................................................................ 2

4. FASES CONCLUÍDAS DO PROJETO ................................................................. 2

4.1. LEVANTAMENTO BIBLIOGRÁFICO DA LITERATURA EXIGIDA PARA A PESQUISA ..... 2 4.1.1. Introdução à Lógica Difusa .......................................................................... 3 4.1.2. O Controlador Difuso ................................................................................... 5

4.2. ESTUDO DA FERRAMENTA DE SOFTWARE NECESSÁRIA PARA A REALIZAÇÃO DO TEMA PROPOSTO ........................................................................................................... 10

4.2.1. Matlab ......................................................................................................... 10 4.2.2. Fuzzy Logic Toolbox ................................................................................... 16

4.3. DEFINIÇÃO E ESPECIFICAÇÃO DAS VARIÁVEIS A SEREM IMPLEMENTADAS .......... 19 4.4. IMPLEMENTAÇÃO DO MÓDULO GERADOR DE FUNÇÕES DE PERTINÊNCIA COM ERRO PROGRAMÁVEL ............................................................................................................. 20

5. RESULTADOS OBTIDOS ATÉ O PRESENTE MOMENTO ......................... 38

6. CONCLUSÕES ...................................................................................................... 38

7. REFERÊNCIAS BIBLIOGRÁFICAS ................................................................. 39

ANEXOS ........................................................................................................................ 41

1

1. Resumo do plano inicial O plano de pesquisa proposto visa o estudo da influência dos erros da função de pertinência no controle lógico difuso. Durante o desenvolvimento do plano, será estudada de uma nova metodologia de controle, a lógica difusa, fornecendo assim ao bolsista a oportunidade fortalecer a sua formação na área de instrumentação e controle.

A lógica difusa foi descrita por L. Zadeh em 1965 sendo descrita como uma lógica de múltiplos valores, em comparação com a lógica tradicional que possui somente uma representação bivalente, ou seja, uma representação de dois valores [1-5]. A lógica difusa é aplicada em qualquer tipo de malha de controle, sendo muito utilizada em sistemas altamente não lineares, onde o modelo matemático do mesmo é difícil de ser obtido. Para se realizar um controle utilizando-se tal lógica é necessário somente a opinião de um especialista no problema, um especialista em lógica difusa e um especialista em software ou hardware. No desenvolvimento deste projeto será utilizado o programa MATLAB 5.0 juntamente com o SIMULINK, da MatWorks Inc. Este programa será utilizado no desenvolvimento de um bloco de fuzzificação de propósito genérico. Ou seja, neste bloco será possível compor qualquer tipo de função de pertinência e atribuir a mesma qualquer tipo de erro. Após a implementação deste bloco o mesmo será transferido para o toolbox fuzzy que se encontra disponível no MATLAB 5.0. Este toolbox possui como principal característica o fato de poder simular sistemas de controle que utilizam a metodologia da lógica difusa. As fases do plano de pesquisa proposto são:

1. Levantamento bibliográfico da literatura exigida para a pesquisa

2. Estudo da ferramenta de software necessária para a realização do tema proposto

3. Definição e especificação das variáveis a serem implementadas

4. Implementação do módulo gerador de funções de pertinência com erro programável

5. Testes do sistema

6. Documentação final

2. Objetivos Fornecer ao bolsista, através do estudo da lógica difusa, os conceitos de uma nova e emergente metodologia na área de controle. O bolsista realizará um estudo das influências dos erros das funções de pertinência no controle exercido através de controladores lógicos difusos implementados em hardware. Este primeiro relatório tem como objetivo a apresentação dos resultados até o presente momento.

2

3. Introdução A análise das influências de erros em funções de pertinência de controladores

lógicos difusos irá facilitar o projeto destes controladores. Com esta análise o projeto poderá simplificado de acordo com o tempo de resposta crítico do controlador, ou seja, o projetista poderá decidir se deve ou não refinar seu projeto para que os erros apresentados nas funções de pertinência não atrapalhem a resposta do seu controlador. Pode-se dizer que este tipo de análise já começa a ser feita sobre outros tipos de erros. Como exemplo podemos citar o artigo[6] publicado recentemente que trata das conseqüências da digitalização em controladores lógicos difusos. Nestes tipos de controladores os sinais e as funções de pertinência são representadas por palavras binárias compostas por um número finito de bits. Neste artigo os autores fazem vários tipos de análises na tentativa de determinar a influência do comprimento da palavra binária em controladores digitalizados. Foram feitas dois tipos de análises, uma análise estatística e uma análise do comportamento de um sistema dinâmico em malha fechada. Na análise estatística os autores chegam à conclusão que o erro médio absoluto entre um controlador lógico contínuo e um controlador lógico digitalizado diminui de uma forma não linear quando a digitalização é refinada. Com a análise do comportamento de um sistema dinâmico em malha fechada algumas distorções nas repostas foram detectadas, sendo que estas distorções diminuem quando a discretização é suficientemente refinada.

Este relatório apresenta parte do trabalho proposto pelo plano de pesquisa. Será apresentado o levantamento bibliográfico, estudo da ferramenta de software necessária para a realização do plano de pesquisa, a definição e especificação das variáveis a serem implementadas e a implementação do módulo gerador de funções de pertinência com erro programável.

4. Fases concluídas do projeto A seguir estão descritas as fases programadas e concluídas pelo bolsista até o presente momento.

4.1. Levantamento bibliográfico da literatura exigida para a pesquisa Para a execução do plano de pesquisa, foi necessário um levantamento bibliográfico, o qual pode ser constituído de estudos baseados em livros, artigos e “sites” da Internet que contenham assuntos relacionados à Lógica Difusa como, por exemplo, projetos de controladores lógicos difusos. As referências bibliográficas selecionadas para o desenvolvimento do projeto de iniciação científica estão citadas na bibliografia, no item 7 deste relatório. O estudo teórico, na área de Lógica Difusa, pode ser realizado através das referências [1], [2], [3], [4], [5], [7], [8], [9], [10], [13] e [16], as quais contém livros técnicos e “sites” da Internet sobre o assunto. Estas referencias foram de grande importância, pois proporcionou um profundo conhecimento do assunto, conhecimento este necessário para que seja possível fazer a análise das influencias dos erros nas funções de pertinência.

3

As aplicações do Lógica Difusa em sistemas que necessitam de sistemas de controle complexos o suficiente, para que a lógica tradicional não consiga propor uma solução, foram estudados pelo bolsista através dos artigos obtidos através de revistas e “sites da Internet” estão indicados nas referencias [11], [12] e [14]. A seguir apresentá-se um resumo do conhecimento adquirido com o levantamento bibliográfico.

4.1.1. Introdução à Lógica Difusa A lógica difusa desenvolvida e proposta por Lotfi Zadeh[1] em 1965 consiste em expressar as leis operacionais de um sistema de controle através de termos lingüísticos, ao invés de equações matemáticas, como ocorre na metodologia clássica, sendo esta, talvez, a sua principal vantagem. Esta lógica é, principalmente, aplicada em sistemas em que o grau de complexidade é tal que a sua modelagem, através de equações matemáticas, torna demasiadamente impreciso o seu controle. Estas imprecisões podem estar relacionadas as não linearidades, variação natural do tempo do processo a ser controlado, ruídos ambientais, degradação dos sensores ou outras dificuldades em obter medidas precisas e de confiança que retratem o real comportamento do sistema. O uso da lógica difusa nesses sistemas complicados utilizam das vantagens inerentes ao uso dos termos lingüisticos, para representá-los corretamente. Esses termos são muitas vezes expressos na forma de implicações lógicas tal como regras contendo: “SE-ENTÃO”. O termo “lógica difusa” (fuzzy logic) fornece a sensação de ser uma metodologia imprecisa onde a exatidão não é necessária ou importante, pois em um mundo grandemente manipulado por computadores, com seus conceitos absolutos de “1” e “0” e “on” e “off”, um termo como lógica difusa sugere inexatidão ou imprecisão. Porém, na prática, esta imprecisão não acontece[7]. A lógica difusa, ao contrário da lógica tradicional, utiliza conhecimentos recebidos a partir de especialistas, profundos conhecedores dos sistemas a serem controlados, para descreverem o funcionamento desses sistemas e orientarem o controle a ser implementado. Porém, o conhecimento a ser recebido dos especialistas também pode não ser transmitido de modo suficientemente claro. Assim, uma descrição lingüistica imprecisa da maneira de se controlar o sistema pode ser usualmente articulada pelo especialista com relativa tranqüilidade. Uma descrição lingüistica fácil de se usar, e que deve ser utilizada como norma pelos especialistas, consiste de um conjunto de regras do tipo:

SE A acontecer e B ocorrer, ENTÃO faça-se C

Comparação entre a lógica difusa e a clássica Para ilustrar a diferença existente entre a lógica difusa e a aproximação tradicional pode-se considerar um rápido exemplo retirado de [7]. Nesse exemplo, um ventilador deve ser controlado baseando-se nas seguintes condições:

SE a temperatura do ar é ³ 70 º Fahrenheit, ENTÃO ajuste a velocidade do ventilador para 1000 rpm

4

SE a temperatura do ar é < 70 º Fahrenheit, ENTÃO ajuste a velocidade do ventilador para 100 rpm

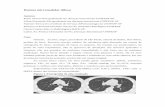
Um controle tradicional confia em um ponto de decisão discreto. Neste caso a entrada precisa alcançar um determinado valor (70 ºF) antes de tomar uma decisão. A figura a seguir mostra o diagrama do controlador tradicional exemplificado acima. Pequenas variações na entrada poderiam causar saídas drasticamente diferentes. É o que aconteceria caso a temperatura variasse em torno de 69,5 º F até 70,5 º F. Estes pontos de transição são críticos para sistemas tradicionais sendo onde a lógica difusa se supera.

Figura 1: Controle tradicional

Na lógica difusa os termos usados são os que se aproximam das condições diárias, como no caso do exemplo, para variáveis de entrada FRIO, MORNO e QUENTE ou para variáveis de saída LENTO, MÉDIO e RÁPIDO. Deste modo, os termos citados acima são parâmetros que definem faixas de valores conhecidos como funções de pertinência, normalmente variando entre 0 e 1. As figuras seguintes mostram as funções de pertinência para variáveis de entrada e saída respectivamente.

Figura 2: Funções de pertinência para variável de entrada

Escolhendo uma faixa de valores ao invés de um simples valor discreto para definir a variável de entrada da temperatura do ar, é possível controlar a variável de saída da velocidade do ventilador mais precisamente. Para descrição desse problema, são utilizadas.regras do tipo:

5

SE a temperatura do ar é MORNO, ENTÃO ajuste a velocidade do ventilador para MÉDIO

Figura 3: Função de pertinência para variável de saída

4.1.2. O Controlador Difuso

Introdução Um controlador difuso é basicamente constituído por 3 blocos, cada bloco correspondendo as seguintes fases:

ü Fuzzificação. ü Inferência ü Defuzzificação

Figura 4: Fases de implementação da lógica difusa

A figura anterior apresenta um diagrama em blocos da seqüência de implementação de um controlador baseado na lógica difusa (fuzzy). Um controlador difuso opera repetindo um ciclo das três fases anteriores. Primeiro as medidas são feitas de todas as variáveis que representam condições relevantes do processo a ser controlado. Depois, essas medidas são convertidas em apropriados conjuntos difusos. Esse passo é chamado de fuzzificação. As medidas fuzzificadas serão então usadas pela fase de inferência para em conjunto com as regras de controle estabelecidas, definirem conjuntos difusos para a fase de defuzzificação. O resultado é um conjunto difuso (ou vários conjuntos difusos) definidos no universo de ações possíveis. O conjunto difuso é então convertido no passo final do ciclo, na fase de defuzzificação, em um simples valor ou vetor de valores. Estes valores defuzzificados representam ações a serem tomadas pelo controlador fuzzy em

6

ciclos de controle individual. Aplicando-se os conceitos aqui colocados no exemplo apresentado anteriormente e analisando cada uma das fases tem-se: Fuzzificação Aplicando-se o exemplo do ventilador citado, tem-se que as funções de pertinência serão: FRIO, QUENTE e MORNO com suas faixas definidas na figura a seguir. Nesta fase são determinados os graus de pertinência, que variam entre 0 e 1, da variável de entrada da “temperatura do ar”, para cada função de pertinência (FRIO, MORNO ou QUENTE). Mais de uma função de pertinência pode estar ativa para uma determinada entrada. Para o exemplo, quando a variável de entrada da temperatura do ar estiver em 70º Fahrenheit implicará na ativação das funções de pertinência QUENTE e MORNO. Nesse caso, tem-se uma pertinência de 0,17 para a função QUENTE e 0,37 para a função MORNO.

Figura 5: Processo de fuzificação

Inferência Uma vez que funções de pertinência tendo sido definidas para variáveis de entrada e saída, uma base de regras de controle deve ser desenvolvida para relatar as ações da saída do controlador para as entradas observadas. Esta fase é conhecida como inferência ou definição das regras para a lógica difusa. Existem dois principais caminhos na qual as regras de inferência relevantes podem ser determinadas. Um modo é deduzir as regras através de operadores humanos experientes[8], e o outro é obter dados empíricos através de métodos de aprendizado adequado, geralmente com o uso de redes neurais[8]. Para o exemplo citado anteriormente, algumas regras podem ser mostradas abaixo:

SE a temperatura do ar é FRIO, ENTÃO ajuste a velocidade do ventilador para LENTO SE a temperatura do ar é QUENTE, ENTÃO ajuste a velocidade do ventilador para RÁPIDO SE a temperatura do ar é MORNO, ENTÃO ajuste a velocidade do ventilador para MÉDIO

7

Da fase de fuzzificação obtém-se as funções que foram ativadas devido ao valor da variável de entrada da temperatura do ar estar em 70 º Fahrenheit. Para esse valor de entrada foram ativadas as funções de pertinência QUENTE e MORNO. Das regras acima tem-se que as funções de pertinência de saída ativadas para esse valor, da variável de entrada da temperatura do ar, são as funções RÁPIDO e MÉDIO respectivamente. Essas regras “SE-ENTÃO” podem relatar múltiplas variáveis de entrada e saída. As regras são baseadas em descrições de palavras ao invés de definições matemáticas. Qualquer relação que possa ser descrita com termos lingüisticos pode tipicamente ser definida por um controlador lógico difuso. Isso significa que sistemas não lineares podem ser descritos e facilmente controlados com um controlador lógico difuso. Diferentes regras tem diferentes impactos no controlador, de acordo com a medida da variável de entrada. Defuzzificação Após o controlador lógico difuso avaliar as entradas e aplicar as regras para estas entradas, é necessário gerar uma saída para o sistema que está sendo controlado. Isso pode significar ajustar uma tensão ou uma corrente para um valor particular, de forma a controlar a velocidade de um ventilador, ou a velocidade ótima de um braço robótico quando ele está próximo do alvo. O controlador lógico difuso necessita converter suas variáveis internas de saída em valores discretos que podem ser usados pelo sistema controlado. Como determinado na fase de inferência, para o valor da variável de entrada da temperatura do ar de 70 º Fahrenheit, as funções de pertinência de saída ativadas foram RÁPIDO e MÉDIO, com pertinências respectivas de 0,37 e 0,17. Dessa forma obtém-se os valores da variável de saída da velocidade do ventilador. Para a função de pertinência RÁPIDO os valores encontrados para a variável de saída foram 680 rpm e 1200 rpm. Para a função de pertinência MÉDIO os valores encontrados para a variável de saída da velocidade do ventilador foram 375rpm e 710 rpm. A figura seguinte ilustra o que foi explicado acima.

Figura 6: Processo de defuzificação

8

Da figura anterior percebe-se que se obteve diversos valores da variável de saída para a velocidade do ventilador. É necessário extrair um valor que seja útil para o sistema. A essa conversão dá-se o nome de defuzzificação. Existem vários métodos de defuzzificação apresentados na literatura [8]. Um dos métodos de defuzzificação utilizado é o método dos máximos. Neste método, o máximo valor de pertinência relativa é usado para determinar o valor numérico para a saída do controlador. Dessa forma, no exemplo aqui utilizado, são encontrados dois valores para essa variável de saída: 375rpm e 710 rpm. Um dos inconvenientes do método de defuzzificação que utiliza os máximos são as soluções múltiplas. Um outro método de defuzificação utilizado é o método do centróide (ou método do centro de gravidade, ou método do centro de área), sendo esse o mais bem conhecido método de defuzificação[9]. Esse método é computacionalmente mais complexo e por esta razão implica em ciclos de inferência mais lentos. Nele todos os valores de pertinência relativas a um valor da variável de entrada são utilizados, formando uma figura geométrica. Dessa forma é calculado o valor do centróide dessa figura geométrica, sendo que, o valor encontrado para o exemplo citado é de 635 rpm. A vantagem do método de defuzzificação do centróide é a eliminação de saídas múltiplas, como no método dos máximos.

Figura 7: Método de defuzzificação do Centróide

O método do menor dos máximos também é usado para se fazer a defuzzificação. Esse método toma o menor valor defuzzificado da máxima pertinência relativa do processo de defuzzificação. Para o caso do exemplo, a máxima pertinência relativa tem o valor de 0,37 e dessa forma os valores defuzzificados obtidos foram 375rpm e 710 rpm, resultando no valor defuzzificado de 375 rpm. Isso é mostrado na figura a seguir.

9

Figura 8: Método de defuzzificação do Menor dos máximos

Por sua vez, o método do maior dos máximos toma o maior valor defuzzificado da máxima pertinência relativa do processo de defuzzificação. Para o caso do exemplo, a máxima pertinência relativa tem o valor de 0,37 e dessa forma os valores defuzzificados obtidos foram 375rpm e 710 rpm, resultando no valor defuzzificado de 710 rpm, que é mostrado na abaixo.

Figura 9: Método de defuzzificação do Maior dos máximos

Figura 10: Método de defuzzificação da Média dos máximos

10

O método da média dos máximos, é muito similar ao método do menor e maior dos máximos. Ao invés de determinar o menor ou o maior valor defuzzificado da máxima pertinência relativa ao processo de defuzzificação, esse método toma média desses dois valores. Dessa forma, o valor defuzzificado obtido, para o exemplo citado, é 542,5 rpm, representado na a seguir.

4.2. Estudo da ferramenta de software necessária para a realização do tema proposto Neste item será apresentada uma breve definição dos tipos operadores e declarações utilizados no Matlab, bem como uma apresentação do Toolbox Fuzzy que serve como base para a realização deste trabalho.

4.2.1. Matlab O Matlab trabalha essencialmente com um tipo de objeto, uma matriz numérica retangular podendo conter elementos complexos (deve-se lembrar que um escalar é uma matriz de dimensão l x l e que um vetor é uma matriz que possui somente uma linha ou uma coluna).

Entrando com Matrizes Simples As matrizes podem ser introduzidas no MATLAB por diferentes caminhos: - digitadas na Janela de Comando (lista explícita de elementos); - - geradas por comandos e funções; - - criadas em arquivos ".m"; - - carregadas a partir de um arquivo de dados externo.

O método mais fácil de entrar com pequenas matrizes no MATLAB é usando uma lista explícita. Os elementos de cada linha da matriz são separados por espaços em branco ou vírgulas e as colunas separadas por ponto e vírgula, colocando-se colchetes em volta do grupo de elementos que formam a matriz. Exemplo: A=[ 1 2 3;4 S 6;7 8 9 ] Outra maneira para entrar com matrizes no MATLAB é através de um arquivo no formato texto com extensão ".m". O comando load pode ler matrizes geradas pelo MATLAB e armazenadas em arquivos binários ou matrizes geradas por outros programas armazenadas em arquivos ASCII.

Elementos das Matrizes Os elementos das matrizes podem ser qualquer expressão do MATLAB, por exemplo.

11

x = [-1.3 sqrt(2) ((1+2+3)*4/5)^2] Um elemento individual da matriz pode ser reverenciado com índice entre parênteses. Continuando o exemplo,

x(6) = abs(x(l)) Grandes matrizes podem ser construídas a partir de pequenas matrizes. Por exemplo, pode-se anexar outra linha na matriz A usando

r= [ l0 11 12]; A= [A;r]

Note que o vetor r não foi listado porque ao seu final foi acrescentado ";". Pequenas, matrizes podem ser extraídas de grandes matrizes usando ";". Por exemplo,

A = A(1:3,:); seleciona as três primeiras linhas e todas as colunas da matriz A atual, modificando-a para sua forma original.

Declarações e Variáveis O MATLAB é uma linguagem de expressões. As expressões usadas são interpretadas e avaliadas pelo sistema. As declarações no MATLAB são freqüentemente da forma

variável = expressão ou simplesmente

expressão As expressões são compostas de operadores e outros caracteres especiais, de funções e dos nomes das variáveis. A avaliação das expressões produzem matrizes, que são então mostradas na tela e atribuídas às variáveis para uso futuro. Se o nome da variável e o sinal de igualdade "=" são omitidos, a variável com o nome ans, que representa a palavra "answer" (resposta), é automaticamente criada. Se a expressão é tão grande que não cabe em apenas uma linha, pode-se continuar a expressão na próxima linha usando um espaço em branco e três pontos,"...", ao final das linhas incompletas. Por exemplo,

s = l - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 + 1/7 ... - 1/8 + 1/9 - l/10 + 1/11 - 1/12 + 1/13;

calcula o resultado da série, atribuindo a somatória à variável s, mas não imprime o resultado na tela. Note que os espaços em branco entre os sinais "=", "+" e "-" são opcionais, mas o espaço em branco entre "1/7" e "..." é obrigatório. As variáveis e funções podem ser formadas por um conjunto de letras, ou por um conjunto de letras e números, onde somente os primeiros 19 caracteres do conjunto são identificados. O MATLAB faz distinção entre letras maiúsculas e minúsculas, assim a e A não são as mesmas variáveis. Todas as funções devem ser escritas em letras minúsculas: inv(A) calcula a inversa de A, mas INV(A) é uma função indefinida.

12

Obtendo Informações da Área de Trabalho Os exemplos de declarações mostrados nos itens acima criaram variáveis que são armazenadas na Área de Trabalho do MATLAB. Executando

who obtêm-se uma lista das variáveis armazenadas na Área de Trabalho. Uma informação mais detalhada mostrando a dimensão de cada uma das variáveis correntes é obtido com whos que para nosso exemplo produz.

Cada elemento de uma matriz real requer 8 bytes de memória, assim nossa matriz A de dimensão 3x3 usa 72 bytes e todas variáveis utilizadas um total de 160 bytes.

Números e Expressões Aritméticas A notação decimal convencional, com ponto decimal opcional e o sinal de menos, é usada para números. A potência de dez pode ser incluída como um sufixo. As expressões podem ser construídas usando os operadores aritméticos usuais e as regras de precedência:

1 ^ exponenciação 2 / divisão a direita 2 \ divisão a esquerda 3 * multiplicação 4 + adição 4 - subtração

Deve-se notar que existem dois símbolos para divisão: as expressões 1/4 e 4\1 possuem o mesmo valor numérico, isto é, 0,25. Parênteses são usados em sua forma padrão para alterar o mesmo a precedência usual dos operadores aritméticos.

Números e Matrizes Complexas Números complexos são permitidos em todas operações e funções no MATLAB. Os números complexos são introduzidos usando-se as funções especiais i e j. Por exemplo

z= 3 + 4*i ou

z= 3 +4*j Outro exemplo é

13

w= r * exp(i*theta) As seguintes declarações mostram dois caminhos convenientes para se introduzir matrizes complexas no MATLAB:

A= [1 2; 3 4]+i*[5 6;7 8] e

A= [1+5*i 2+6*i; 3+7*i 4+8*i] que produzem o mesmo resultado. Se i ou j forem usados como variáveis, de forma que tenham seus valores originais modificados, uma nova unidade complexa deverá ser criada e utilizada de maneira usual:

ii = sqrt(-1); z = 3 + 4*ii

Formato de Saída O formato numérico exibido na tela pode ser modificado utilizando-se o comando format, que afeta somente o modo como as matrizes são mostradas, e não como elas são computadas ou salvas (o MATLAB efetua todas operações em dupla precisão). Se todos os elementos das matrizes são inteiros exatos, a matrizes é mostrada em um formato sem qualquer ponto decimal. Por exemplo,

x = [-1 0 1] sempre resulta em

x = -1 0 1 Se pelo menos um dos elementos da matriz não é inteiro exato, existem várias possibilidades de formatar a saída. O formato "default", chamado de formato short, mostra aproximadamente 5 dígitos significativos ou usam notação científica. Por exemplo a expressão

x = [4/3 1.2345e-6]

é mostrada , para cada formato usado, da seguinte maneira: format short 1.3333 0.0000 format short e 1.3333e+000 1.2345e-006 format long 1.33333333333333 0.000000123450000 format long e 1.333333333333333e+000 1.234500000000000e-006 format hex 3ff5555555555555 3eb4b6231abfd271

14

format rat 4/3 1/810045 format bank 1.33 0.00 format + ++

Com o formato short e long, se o maior elemento da matriz é maior que 1000 ou menor que 0.001, um fator de escala comum é aplicado para que a matriz completa seja mostrada. Por exemplo,

x = 1.e20*x resultado da multiplicação será mostrado na tela.

X = l.0e+20 * 1.3333 0.0000 O formato + é uma maneira compacta de mostrar matrizes de grandes dimensões. Os símbolos "+", "-", e "espaço em branco" são mostrados, respectivamente para elementos positivos, elementos negativos e zeros.

As Facilidades do HELP (Ajuda) O MATLAB possui um comando de ajuda (help) que fornece informações sobre a maior parte dos tópicos. Digitando

help obtêm-se uma lista desses tópicos disponíveis: HELP topics: c:\matlab -Establish MATLAB session parameters. matlab\general -General purpose commands. matlab\ops -Operators and special characters. matlab\lang -Language constructs and debugging. matlab\elmat -Elementary matrices and matrix manipulation. matlab\specmat -Specialized matrices. matlab\elfun -Elementary math functions. matlab\specfun -Specialized math functions. matlab\matfun -Matrix functions - numerical linear algebra. matlab\datafun -Data analysis and Fourier transform functions. matlab\polyfun -Polynomial and interpolation functions. matlab\funfun -Function functions: nonlinear numerical methods. matlab\sparfun -Sparse matrix functions. matlab\plotxy -Two dimensional graphics. matlab\piotxyz -Three dimensional graphics. matlab\graphics -General purpose graphics functions. matlab\color -Color control and lighting model functions. matlab\sounds -Sound processing functions.

15

matlab\strfun -Character string functions. matlab\iofun -Low-level file I/0 functions. matlab\demos -Demonstrations and samples. simulink\simulink -SIMULINK model analysis. simulink\blocks -SIMULINK block library. simulink\simdemos -SIMULINK demonstrations and samples. nnet\exampies - Neural Network Toolbox examples. nnet\nnet - Neural Network Toolbox.

For more help on directory/topic, type 'help topic".

Para obter informações sobre um tópico específico, digite help tópico. Por exemplo,

help plotxy que fornece uma lista de todos os comandos relacionados com gráficos bidimensionais:

Two dimensional graphics. Elementary X-Y graphs plot - Linear plot. loglog - Log-log scafe plot. semilogx - Semi-log scale plot. semilogy - Semi-log scale plot. fill - Draw filled 2-D polygons. Specialized X-Y graphs. polar - Polar coordinate plot. bar - Bar graph. stem - Discrete sequence or & "stemm" plot. stairs - Stairstep plot. errorbar - Error bar plot. hist - Histogram plot. rose - Angle histogram plot. compass - Compass plot. feather - Feather plot. fplot - Plot function comet - Comet-like trajectory. Graph annotation. title - Graph title. xlabel - X-axis label. ylabel - Y-axis label. text - Text annotation. gtext - Mouse placement of text. grid - Grid lines. See also PLOTXYZ, GRAPHICS

16

Finalmente, para obter informações sobre um comando específico, por exemplo title, digite: help title e informações mais detalhadas sobre este comando serão exibidas: TITLE Titles for 2-D and 3-D plots. TITLE (‘text’) adds text at the top of the current axis. See also XLABEL, YLABEL, ZLABEL, TEXT. Note que no exemplo mostrado para adicionar o título em um gráfico, TITLE (‘TEXT’) está escrito em letras maiúsculas somente para destacar. Deve-se lembrar que todos os comandos do MATLAB devem ser escritas em letras minúsculas, portanto, para adicionar o texto "Título do Gráfico" em um gráfico, digite:

title (‘Título do Gráfico’)

Funções A "força" do MATLAB vem de um conjunto extenso de funções. O MATLAB possui um grande número de funções intrínsecas que não podem ser alteradas pelo usuário. Outras funções estão disponíveis em uma biblioteca externa distribuídas com o programa original (MATLAB TOOLBOX), que são na realidade arquivos com a extensão ".m" criados a partir das funções intrínsecas. A biblioteca externa (MATLAB TOOLBOX) pode ser constantemente atualizada à medida que novas aplicações são desenvolvidas. As funções do MATLAB, intrínsecas ou arquivos ".m", podem ser utilizadas apenas no ambiente MATLAB.

4.2.2. Fuzzy Logic Toolbox Sobre este toolbox podemos fazer uma breve apresentação.

O toolbox fuzzy é dividido em três partes: 1. Funções de linha de comando; 2. Ferramentas gráficas interativas; 3. blocos e exemplos no Simulink.

Até o presente momento só foram utilizadas as partes 1 e 2 do toolbox. Sendo que a parte 1 é composta por todas as funções escritas na linguagem utilizada pelo Matlab e a segunda parte agrega todas estas funções em uma interface gráfica de ótima interatividade com o usuário. A parte gráfica é dividida nas seguintes partes:

ü FIS editor => É nesta parte que se inicia a criação do sistema de inferência, aqui pode-se escolher o tipo de defuzificação, o método utilizado na inferência, definir o número de variáveis de entrada e saída, dentre outras funções.

17

Figura 11: Editor do Sistema de Inferência Difuso - FIS Editor

ü Membership Function Editor => Nesta parte são escolhidas as funções de pertinência para as entradas e saídas do sistema.

Figura 12:Editor de Funções de Pertinência – Membership Function Editor

ü Rule Editor => Aqui pode-se escrever as regras do sistema de 3 formas: a forma escrita (Ex.: If(service is poor)then(tip is cheap)(1)), a forma simbólica (Ex.: 1.(service==poor)=>(tip=cheap)(1)) e a forma indexado (Ex.: 1,1(1):1).

18

Figura 13:Editor de Regras – Rule Editor

ü Rule Viewer => Nesta parte pode-se ver graficamente a influência das regras criadas no Rule Editor na saída do sistema de acordo com a entrada setada.

Figura 14: Visualizador de Regras – Rule Viewer

ü Surface Viewer => Nesta última parte pode-se ver a superfície de controle do sistema, baseado em todas as variáveis setadas nas partes anteriores do toolbox.

19

Figura 15:Visualizador de Superfície – Surface Viewer

Para o estudo deste Toolbox do Matlab foi utilizado o Manual que acompanha este produto referido na seção de referencias bibliográficas em [15].

4.3. Definição e especificação das variáveis a serem implementadas Foi definido que inicialmente serão analisados os erros verificados em funções de pertinência do tipo triangular. O tipos de erros básicos que devem ser implementados e estudados são mostrados na figura a seguir.

Figura 16:Exemplo de erros em funções de pertinência do tipo Triangular

Uma aproximação matemática escolhida, de acordo com as especificações das funções que o “toolbox fuzzy” utiliza, foi a equação de uma parábola em substituição a equação da reta que produz os lados da função triangular.

20

Para a execução dos teste foi utilizado um sistema lógico difuso presente no próprio “toolbox” um sistema para se determinar a gorjeta a ser dada para um garçom em função das entradas Qualidade da comida e Qualidade do Atendimento.

4.4. Implementação do módulo gerador de funções de pertinência com erro programável

De acordo com as modificações feitas no “toolbox“ pode gerar as seguintes alterações na função de pertinência do tipo triangular:

Figura 17:Erros na função de pertinência triangular; (a)Alterações em ambos os lados do

triângulo, convexo - convexo e côncavo – côncavo; (b)Alterações em ambos os lados do triângulo, côncavo - convexo e convexo – côncavo; (c)Alterações em apenas um lado do

triângulo, normal - côncavo e côncavo – normal; (d)Alterações em apenas um lado do triângulo, normal - convexo e convexo – normal

Estas modificações foram feitas através da edição de algumas linhas de código dos seguintes arquivos:

21

ü Trimf.m: Este arquivo é responsável pela geração da função de pertinência triangular, foi então adicionado mais um parâmetro, sendo que este determina o tipo de erro que se deseja gerar na função triangular.

ü Mf2mf.m: Este arquivo é responsável pela conversão entre os diversos tipos de funções de pertinência, foi alterado de modo a reconhecer o parâmetro adicionado no arquivo anterior.

Após estas modificações surgiu a necessidade de se criar um programa que apresentasse uma superfície de erro. Este programa funciona da seguinte forma: primeiro a função de pertinência deve ser alterada de acordo com os erros que se desejam avaliar, o sistema completo deve ser salvo com um nome diferente do original, depois executa-se o programa gravado no arquivo “errorfis.m”. Após este processo pode gerar uma superfície de erro absoluto e erro relativo. A superfície de erro absoluto foi gerada subtraindo-se todos os pontos da superfície com erro da superfície original e a superfície de erro relativo foi gerada dividindo-se o resultado da operação anterior pelos pontos da superfície original. Um exemplo disto pode ser mostrado através das figuras a seguir, geradas com a utilização de um sistema de demonstração (tipper.fis) incluso no “toolbox fuzzy”.

Figura 18:Funções de pertinência da entrada 1 (“Service”) do sistema original

22

Figura 19:Superfície final do sistema original sem erros

As figuras anteriores mostram as funções de pertinência originais e a superfície original do sistema anteriormente citado. E as figuras seguintes mostram o mesmo sistema com as mesmas regras, variáveis de entrada e saída, mas com a função de pertinência da entrada 1 alterada com os diversos erros possíveis de serem gerados com as modificações feitas no “toolbox”.

Figura 20:Funções de pertinência com alterações do tipo convexo-convexo

23

Figura 21:Superfície final do sistema com alterações do tipo convexo-convexo

Figura 22:Superfície que representa o desvio percentual absoluto entre o sistema original e o

sistema com erros

Pode-se observar através da figura anterior que o erro gerado, produz um desvio máximo de cerca de 200% acima e abaixo do valor original verificado na superfície original.

24

Figura 23:Superfície que representa o desvio percentual relativo ao sistema original

Como era de se esperar o erro relativo apresenta valores menores que os apresentados pela superfície de erro percentual absoluto. Estes valores se situam entre cerca de 10% acima do valor original e 15% abaixo deste valor.

Figura 24: Funções de pertinência com alterações do tipo côncavo-côncavo

25

Figura 25: Superfície final do sistema com alterações do tipo côncavo-côncavo


sistema com erros

26


Figura 28: Funções de pertinência com alterações do tipo côncavo-convexo

27

Figura 29: Superfície final do sistema com alterações do tipo côncavo-convexo


sistema com erros

28


Figura 32: Funções de pertinência com alterações do tipo convexo-côncavo

29

Figura 33: Superfície final do sistema com alterações do tipo convexo-côncavo


sistema com erros

30


Figura 36: Funções de pertinência com alterações do tipo normal-côncavo

31

Figura 37: Superfície final do sistema com alterações do tipo normal-côncavo


sistema com erros

32


Figura 40: Funções de pertinência com alterações do tipo côncavo-normal

33

Figura 41: Superfície final do sistema com alterações do tipo côncavo-normal


sistema com erros

34


Figura 44: Funções de pertinência com alterações do tipo normal-convexo

35

Figura 45: Superfície final do sistema com alterações do tipo normal-convexo


sistema com erros

36


Figura 48: Funções de pertinência com alterações do tipo convexo-normal

37

Figura 49 : Superfície final do sistema com alterações do tipo convexo-normal


sistema com erros

38


Obs.: Os respectivos códigos dos arquivos citados neste item estão presentes no anexo I.

5. Resultados obtidos até o presente momento Até o presente momento os resultados obtidos pelo bolsista podem ser considerados positivos, uma vez que durante as várias etapas por que passou, os diversos tópicos estudados e analisados contribuíram significativamente para o aprimoramento da formação de um futuro engenheiro. Durante as diversas fases algumas ferramentas de “software” tiveram que ser estudados como:

ü Matlab – Utilizado na execução dos programas de simulação de sistemas lógicos difusos (“Fuzzy Logic Toolbox”) e do programa para obtenção das superfícies de erro. ü “Fuzzy Logic Toolbox” – Utilizado como ferramenta de simulação dos sistemas lógicos difusos com uma interface gráfica com muitos recursos de simulação e visualização.

6. Conclusões Até o presente momento, acredita-se que foram estudados diversos assuntos extremamente importantes para a formação do bolsista, não só pela utilização da ferramenta Matlab como na área de projeto de controladores lógicos difusos.

39

Neste relatório está incluído também a quarta parte do cronograma proposto inicialmente. Este adiantamento ocorreu porque a terceira fase do projeto acabou se mesclando com a quarta parte, devido à interdependência das mesmas, identificada durante a pesquisa das alterações possíveis do “toolbox Fuzzy”. Portanto para que as variáveis a serem implementadas pudessem ser especificadas, primeiramente foi necessário identificar as capacidades de implementação do citado “toolbox”. Nos próximos seis meses, o bolsista pretende cumprir o restante do cronograma, aperfeiçoando a interface do programa gerador de erros e se aprimorar nas técnicas de projeto de circuitos lógicos difusos. Além disto pretende-se analisar o comportamento de um sistema de controle em função dos diversos erros e diversos tipos de função aqui apresentados.

________________________ ________________________ Fernando Setra Dantas Galdenoro Botura Jr.

Bolsista Orientador

7. Referências Bibliográficas [1] Zadeh, L, Fuzzy Sets, Information and Control, no 8, 338-353, 1965. [2] Zadeh, L, Making computers think like people, IEEE Spectrum, August 1984. [3] Sugeno, M., An Introduction Survey of Fuzzy Control, Information Sciences 36, 59-83, 1985. [4] Zadeh, L., Fuzzy Logic, IEEE, April 1988. [5] Pedrycz, W. and Gomide, F., An Introduction to Fuzzy Sets – Analysis and Design, MIT Press – Cambridge, 1998. [6]Campo, Inés del and Tarela, José Manuel, “Consequences of the Digitization on the Performance of a Fuzzy Logic Controler”, IEEE, February 1999. [7] Timothy A. Adcock, “Digital Signal Processing”, Semiconductor Group, Texas Instruments Incorporated, Janeiro 1993. [8] Klir, G. J., Yuan, B., “Fuzzy Sets and Fuzzy Logic - Theory and Aplications”, Prentice Hall, pp 333-334, 1995 [9] D. Driankov, H. Hellendoorn, M. Reinfrank, “An Introduction to Fuzzy Control”, Springer, 2ªedição, pp134, 1996

40

[10] “Fuzzy Logic” - http://www.abo.fi/~rfuller/fuzs.html [11] “Fuzzy Logic Sources of Information” - http://www.cms.dmu.ac.uk/~rij/fuzzy.html [12] “Artificial Intelligence Publications” - http://oingo.com/topic/11/11993.html [13] Berkan, Riza C. and Trubatch, Sheldon L., “Fuzzy Systems Design Principles” [14]Schwartz, Daniel G. and Klir, George J., “Fuzzy Logic Flowers i Japan”, IEEE Spectrum, July 1992. [15] Gulley, Ned and Jang,J.S. Roger, “Fuzzy Logic Toolbox for use with MATLAB” [16]

41

ANEXOS

42

Arquivo do programa Trimf.m: function y = trimf(x, params) %TRIMF Triangular membership function. % TRIMF(X, PARAMS) returns a matrix which is the triangular % membership function evaluated at X. PARAMS = [A B C] is a 3-element % vector that determines the break points of this membership function. % Usually we require A <= B <= C. % % Note that this MF always has a height of unity. To have a triangular % MF with a height less than unity, use TRAPMF instead. % % For example: % % x = (0:0.2:10)'; % y1 = trimf(x, [3 4 5]); % y2 = trimf(x, [2 4 7]); % y3 = trimf(x, [1 4 9]); % subplot(211), plot(x, [y1 y2 y3]); % y1 = trimf(x, [2 3 5]); % y2 = trimf(x, [3 4 7]); % y3 = trimf(x, [4 5 9]); % subplot(212), plot(x, [y1 y2 y3]); % set(gcf, 'name', 'trimf', 'numbertitle', 'off'); % % See also DSIGMF, GAUSS2MF, GAUSSMF, GBELLMF, EVALMF, PIMF, PSIGMF, % SIGMF, SMF, TRAPMF, ZMF. % Roger Jang, 6-29-93, 10-5-93, 4-14-94. % Copyright (c) 1994-96 by The MathWorks, Inc. % $Revision: 1.11 $ $Date: 1996/04/02 23:21:40 $ if nargin ~= 2 error('Two arguments are required by the triangular MF.'); elseif length(params) < 4 error('The triangular MF needs at least three parameters.'); end a = params(1); b = params(2); c = params(3); erro = params(4); n = 8;%params(5); if a > b, error('Illegal parameter condition: a > b'); elseif b > c, error('Illegal parameter condition: b > c'); elseif a > c, error('Illegal parameter condition: a > c'); end y = zeros(size(x)); % Left and right shoulders (y = 0) index = find(x <= a | c <= x); y(index) = zeros(size(index)); % Left slope

43

if (a ~= b) index = find(a < x & x < b); if (erro==0|erro==16|erro==32) y(index) = (x(index)-a)/(b-a); elseif (erro==4|erro==20|erro==36) z(index) =(x(index)-a)/(b-a); y(index) = z(index).^n; elseif (erro==8|erro==24|erro==40) z(index) =(x(index)-b)/(a-b); y(index) = 1-z(index).^n; else error('Illegal parameter'); end end % right slope if (b ~= c) index = find(b < x & x < c); if (erro==0|erro==4|erro==8) y(index) = (c-x(index))/(c-b); elseif (erro==16|erro==20|erro==24) z(index) =(x(index)-b)/(c-b); y(index) =1-z(index).^n; elseif (erro==32|erro==36|erro==40) z(index) =(x(index)-c)/(b-c); y(index) = z(index).^n; else error('Illegal parameter'); end end % Center (y = 1) index = find(x == b); y(index) = ones(size(index));

44

Arquivo do programa Mf2mf.m: function [outParams,errorStr]=mf2mf(inParams,inType,outType) %MF2MF Translate parameters between functions. % outParams=MF2MF(inParams,inType,outType) takes the original % membership function parameters and type and returns parameters % appropriate to the new membership function type. The result % is very rough approximation of the general location and shape % of the original. % % For example: % % x = (0:0.1:10)'; % pOld = [1.5 5]; % y1 = gaussmf(x,pOld); % pNew = mf2mf(pOld,'gaussmf','trimf'); % y2 = trimf(x,pNew); % plot(x,y1,'y',x,y2,'c') % title('MF Conversion') % % See also DSIGMF, GAUSSMF, GAUSS2MF, GBELLMF, EVALMF, PIMF, % PSIGMF, SIGMF, SMF, TRAPMF, TRIMF, ZMF. % Ned Gulley, 6-17-94 % Copyright (c) 1994-96 by The MathWorks, Inc. % $Revision: 1.15 $ $Date: 1996/07/25 18:35:12 $ yWaist=0.5; yShoulder=0.90; outParams=[]; errorStr=[]; if strcmp(inType,'trimf'), lftWaist=yWaist*(inParams(2)-inParams(1))+inParams(1); lftShoulder=yShoulder*(inParams(2)-inParams(1))+inParams(1); rtShoulder=(1-yShoulder)*(inParams(3)-inParams(2))+inParams(2); rtWaist=(1-yWaist)*(inParams(3)-inParams(2))+inParams(2); elseif strcmp(inType,'trapmf') | strcmp(inType,'pimf'), lftWaist=yWaist*(inParams(2)-inParams(1))+inParams(1); lftShoulder=yShoulder*(inParams(2)-inParams(1))+inParams(1); rtShoulder=(1-yShoulder)*(inParams(4)-inParams(3))+inParams(3); rtWaist=(1-yWaist)*(inParams(4)-inParams(3))+inParams(3); elseif strcmp(inType,'gaussmf'), lftWaist=-abs(inParams(1))*sqrt(-2*log(yWaist))+inParams(2); lftShoulder=-abs(inParams(1))*sqrt(-2*log(yShoulder))+inParams(2); rtShoulder=2*inParams(2)-lftShoulder; rtWaist=2*inParams(2)-lftWaist; elseif strcmp(inType,'gauss2mf'), lftWaist=-abs(inParams(1))*sqrt(-2*log(yWaist))+inParams(2); lftShoulder=inParams(2); rtShoulder=inParams(4); rtWaist=abs(inParams(3))*sqrt(-2*log(yWaist))+inParams(4); elseif strcmp(inType,'gbellmf'),

45

lftWaist=-inParams(1)*((1/yWaist-1)^(1/(2*inParams(2))))+inParams(3); lftShoulder=-inParams(1)*((1/yShoulder-1)^(1/(2*inParams(2))))+inParams(3); rtShoulder=2*inParams(3)-lftShoulder; rtWaist=2*inParams(3)-lftWaist; elseif strcmp(inType,'sigmf'), if inParams(1)>0, lftWaist=inParams(2); lftShoulder=-1/inParams(1)*log(1/yShoulder-1)+inParams(2); rtShoulder=2*lftShoulder-lftWaist; rtWaist=2*rtShoulder-lftWaist; else rtWaist=inParams(2); rtShoulder=-1/inParams(1)*log(1/yShoulder-1)+inParams(2); lftShoulder=rtShoulder; lftWaist=2*lftShoulder-rtWaist; end elseif strcmp(inType,'dsigmf'), lftWaist=inParams(2); lftShoulder=-1/inParams(1)*log(1/yShoulder-1)+inParams(2); rtWaist=inParams(4); rtShoulder=1/inParams(3)*log(1/yShoulder-1)+inParams(4); elseif strcmp(inType,'psigmf'), lftWaist=inParams(2); lftShoulder=-1/inParams(1)*log(1/yShoulder-1)+inParams(2); rtWaist=inParams(4); rtShoulder=-1/inParams(3)*log(1/yShoulder-1)+inParams(4); elseif strcmp(inType,'smf'), lftWaist=yWaist*(inParams(2)-inParams(1))+inParams(1); lftShoulder=yShoulder*(inParams(2)-inParams(1))+inParams(1); rtShoulder=inParams(2); if inParams(1)<inParams(2), lftWaist=inParams(1); rtWaist=2*inParams(2)-inParams(1); else lftWaist=2*inParams(2)-inParams(1); rtWaist=inParams(1); end elseif strcmp(inType,'zmf'), lftShoulder=inParams(2); rtShoulder=inParams(2); if inParams(1)<inParams(2), lftWaist=inParams(1); rtWaist=2*inParams(2)-inParams(1); else lftWaist=2*inParams(2)-inParams(1); rtWaist=inParams(1); end else % Input MF type is unknown outParams=[]; errorStr=['Cannot translate from input MF type ' inType]; if nargout<2, error(errorStr); end

46

return end % We've translated into generalized coordinates, now translate back into % MF specific parameters... if strcmp(outType,'trimf'), center=(rtShoulder+lftShoulder)/2; % Assumes yWaist=0.5 outParams=[2*lftWaist-center center 2*rtWaist-center 0 2]; elseif strcmp(outType,'trapmf')|strcmp(outType,'pimf'), % Assumes yWaist=0.5 outParams=[2*lftWaist-lftShoulder lftShoulder rtShoulder 2*rtWaist-rtShoulder]; elseif strcmp(outType,'gbellmf'), center=(rtShoulder+lftShoulder)/2; a=center-lftWaist; b=2*a/(lftShoulder-lftWaist); outParams=[a b center]; elseif strcmp(outType,'gaussmf'), center=(rtShoulder+lftShoulder)/2; sigma=(rtWaist-center)/sqrt(-2*log(yWaist)); outParams=[sigma center]; elseif strcmp(outType,'gauss2mf'), lftSigma=(lftShoulder-lftWaist)/sqrt(-2*log(yWaist)); rtSigma=(rtWaist-rtShoulder)/sqrt(-2*log(yWaist)); outParams=[lftSigma lftShoulder rtSigma rtShoulder]; elseif strcmp(outType,'sigmf'), center=lftWaist; a=-1/(lftShoulder-center)*log(1/yShoulder-1); outParams=[a center]; elseif strcmp(outType,'dsigmf'), lftCenter=lftWaist; lftA=-1/(lftShoulder-lftCenter)*log(1/yShoulder-1); rtCenter=rtWaist; rtA=1/(rtShoulder-rtCenter)*log(1/yShoulder-1); outParams=[lftA lftCenter rtA rtCenter]; elseif strcmp(outType,'psigmf'), lftCenter=lftWaist; lftA=-1/(lftShoulder-lftCenter)*log(1/yShoulder-1); rtCenter=rtWaist; rtA=-1/(rtShoulder-rtCenter)*log(1/yShoulder-1); outParams=[lftA lftCenter rtA rtCenter]; %keyboard elseif strcmp(outType,'smf'), % Assumes yWaist=0.5 outParams=[2*lftWaist-lftShoulder lftShoulder]; elseif strcmp(outType,'zmf'), % Assumes yWaist=0.5

47

outParams=[rtShoulder 2*rtWaist-rtShoulder]; %elseif strcmp(outType,'psigmf'), % lftCenter=(lftWaist+lftShoulder)/2; % lftA=abs(-1/(lftWaist-lftCenter)*log(1/yWaist-1)); % rtCenter=(rtWaist+rtShoulder)/2; % rtA=-abs(-1/(rtWaist-rtCenter)*log(1/yWaist-1)); % outParams=[lftA lftCenter rtA rtCenter]; else % Output MF type is unknown outParams=[]; errorStr=['Cannot translate to output MF type ' outType]; if nargout<2, error(errorStr); end return end outParams=eval(mat2str(outParams,4));

48

Arquivo do programa Errorfis.m close all; clear all; a=readfis('normal'); b=readfis('erro'); [x1 y1 z1]=gensurf(a); [x2 y2 z2]=gensurf(b); x3=x1; y3=y1; z3=100.*(z1-z2); x4=x1; y4=y1; z4=100.*((z1-z2)./z1); figure(6) surf(x1,y1,z1) xlabel('entrada 1'); ylabel('entrada 2'); zlabel('saída'); title('Superfície Original'); figure(7) surf(x2,y2,z2) xlabel('entrada 1'); ylabel('entrada 2'); zlabel('saída'); title('Superfície com Erro'); figure(8) surf(x3,y3,z3) xlabel('entrada 1'); ylabel('entrada 2'); zlabel('erro em %'); title('Desvio %'); %colormap('gray') %shading interp; %axis([0 10 0 10 -200 200]) rotate3d on; figure(9) surf(x4,y4,z4) xlabel('entrada 1'); ylabel('entrada 2'); zlabel('erro em %'); title('Desvio relativo'); rotate3d on;

Universidade Estadual Paulista “Júlio de Mesquita Filho”

UNESP

Faculdade de Engenharia de Guaratinguetá Departamento de Engenharia Elétrica

Estudo da influência dos erros da função de pertinência no controle lógico difuso

Autor: Fernando Setra Dantas Orientador: Prof. Dr. Galdenoro Botura Jr.

Novembro de 2000

ÍNDICE

1. RESUMO DO PLANO INICIAL ........................................................................... 1 2. RESUMO DO RELATÓRIO ANTERIOR – MAIO DE 2000 ............................ 2 3. FASES CONCLUÍDAS DO PROJETO ................................................................. 3

3.1. IMPLEMENTAÇÃO DO MÓDULO GERADOR DE FUNÇÕES DE PERTINÊNCIA COM ERRO PROGRAMÁVEL ............................................................................................................... 3

4. TESTE DO SISTEMA ............................................................................................. 6 4.1. PRIMEIRA FASE DE TESTES .................................................................................. 11

4.1.1. Erro tipo 1 – Convexo-Convexo ................................................................. 11 4.1.2. Erro tipo 2 – Côncavo-Côncavo ................................................................. 12 4.1.3. Erro tipo 3 – Côncavo-Convexo ................................................................. 12 4.1.4. Erro tipo 4 – Convexo-Côncavo ................................................................. 13 4.1.5. Erro tipo 5 – Normal-Côncavo ................................................................... 14 4.1.6. Erro tipo 6 – Côncavo-Normal ................................................................... 14 4.1.7. Erro tipo 7 – Normal-Convexo ................................................................... 15 4.1.8. Erro tipo 8 – Convexo-Normal ................................................................... 16

4.2. SEGUNDA FASE DE TESTES .................................................................................. 16 4.2.1. Erro tipo 1 – Convexo-Convexo ................................................................. 17 4.2.2. Erro tipo 2 – Côncavo-Côncavo ................................................................. 17 4.2.3. Erro tipo 3 – Côncavo-Convexo ................................................................. 18 4.2.4. Erro tipo 4 – Convexo-Côncavo ................................................................. 19 4.2.5. Erro tipo 5 – Normal-Côncavo ................................................................... 20 4.2.6. Erro tipo 6 – Côncavo-Normal ................................................................... 21 4.2.7. Erro tipo 7 – Normal-Convexo ................................................................... 22 4.2.8. Erro tipo 8 – Convexo-Normal ................................................................... 23

4.3. ANÁLISE GERAL .................................................................................................. 24

5. CONCLUSÕES ...................................................................................................... 25 6. REFERÊNCIAS BIBLIOGRÁFICAS ................................................................. 26 ANEXOS ........................................................................................................................ 27

1

1. Resumo do plano inicial

O plano de pesquisa proposto visa o estudo da influência dos erros da função de pertinência no controle lógico difuso. Durante o desenvolvimento do plano, será estudada de uma nova metodologia de controle, a lógica difusa, fornecendo assim ao bolsista a oportunidade fortalecer a sua formação na área de instrumentação e controle.

A lógica difusa foi descrita por L. Zadeh em 1965 sendo descrita como uma

lógica de múltiplos valores, em comparação com a lógica tradicional que possui somente uma representação bivalente, ou seja, uma representação de dois valores [1-5]. A lógica difusa é aplicada em qualquer tipo de malha de controle, sendo muito utilizada em sistemas altamente não lineares, onde o modelo matemático do mesmo é difícil de ser obtido.

Para se realizar um controle utilizando-se tal lógica é necessário somente à opinião de um especialista no problema, um especialista em lógica difusa e um especialista em software ou hardware.

No desenvolvimento deste projeto será utilizado o programa MATLAB 5.0

juntamente com o SIMULINK, da MatWorks Inc. Este programa será utilizado no desenvolvimento de um bloco de difusão de propósito genérico. Ou seja, neste bloco será possível compor qualquer tipo de função de pertinência e atribuir a mesma qualquer tipo de erro. Após a implementação deste bloco o mesmo será transferido para o toolbox fuzzy que se encontra disponível no MATLAB 5.0. Este toolbox possui como principal característica o fato de poder simular sistemas de controle que utilizam a metodologia da lógica difusa.

As fases do plano de pesquisa proposto são:

1. Levantamento bibliográfico da literatura exigida para a pesquisa

2. Estudo da ferramenta de software necessária para a realização do tema proposto

3. Definição e especificação das variáveis a serem implementadas

4. Implementação do módulo gerador de funções de pertinência com erro programável

5. Testes do sistema

6. Documentação final

2

2. Resumo do relatório anterior – Maio de 2000

O primeiro relatório teve como objetivo principal, a apresentação do progresso deste bolsista frente ao plano de pesquisa.

Como proposta do projeto tem-se a análise das influências de erros em funções

de pertinência de controladores lógicos difusos, que irá facilitar o projeto de circuitos integrados desta classe de controladores. Com esta análise, o projeto poderá ser simplificado de acordo com o tempo de resposta crítico do controlador, ou seja, o projetista poderá decidir se deve ou não refinar seu projeto para que os erros apresentados nas funções de pertinência não atrapalhem a resposta do seu controlador. Pode-se dizer que este tipo de análise já começa a ser feita sobre outros tipos de erros.

Como exemplo pode-se citar o artigo[6] ,publicado recentemente, que trata das

conseqüências da digitalização em controladores lógicos difusos. Nestes tipos de controladores os sinais e as funções de pertinência são representadas por palavras binárias compostas por um número finito de bits. Neste artigo os autores fazem vários tipos de análises na tentativa de determinar a influência do comprimento da palavra binária em controladores digitalizados. Foram feitos dois tipos de análises, uma análise estatística e uma análise do comportamento de um sistema dinâmico em malha fechada.

Na análise estatística os autores chegam à conclusão que o erro médio absoluto

entre um controlador lógico contínuo e um controlador lógico digitalizado diminui de uma forma não linear quando a digitalização é refinada. Com a análise do comportamento de um sistema dinâmico em malha fechada algumas distorções nas repostas foram detectadas, sendo que estas distorções diminuem quando a discretização é suficientemente refinada.

No relatório também é mostrado o progresso feito pelo bolsista até aquele

momento, com uma introdução à lógica difusa e ao controlador difuso feita utilizando os conhecimentos adquiridos com o levantamento bibliográfico.

Com a finalidade de apresentar o que foi estudado sobre as ferramentas a serem

utilizadas, foi feita uma introdução aos conceitos e comandos do software MATLAB e uma breve descrição do “Fuzzy Logic Toolbox” onde constam suas características, divisões e métodos de utilização.

Com o término do estudo da lógica difusa e dos softwares que foram utilizados

neste projeto foi possível passar para a fase seguinte, onde foram definidas as variáveis a serem implementadas no projeto do módulo de difusão e a forma de implementação destas variáveis.

Como última realização do projeto naquele momento, foram mostradas as

modificações feitas no “Fuzzy Logic Toolbox” e os métodos utilizados para possibilitar estas modificações .

3

Este relatório apresentará a conclusão do trabalho proposto pelo plano de pesquisa. Serão apresentadas as modificações feitos no módulo gerador de funções de pertinência com erro programável e os testes feitos com este módulo.

3. Fases concluídas do projeto

A seguir estão descritas as fases finais do projeto que foram devidamente executadas pelo bolsista.

3.1. Implementação do módulo gerador de funções de pertinência com erro programável

Apesar desta fase já estar apresentada e discutida no primeiro relatório, será novamente inserida neste relatório devido às modificações feitas no módulo gerador de erro com a finalidade de facilitar o uso do mesmo pelo usuário.

Os erros de uma função de pertinência triangular podem ser gerados como

mostrados na figura 1, sendo: Lado esquerdo (inclinação positiva)

( )( )ab

axy

−

−= (1)

Lado direito (inclinação negativa)

( )( )bc

xcy

−

−= (2)

onde as variáveis a, b, c, e x, estão referenciadas na figura 2.

As alterações presentes no módulo apresentado no relatório anterior permitem

que o usuário do módulo, quando desejar estudar a influência de um determinado tipo de erro na função, determine este tipo de erro e o valor percentual do erro através da inserção de dados como parâmetros de uma função de pertinência triangular.

No sistema original as equações que definiam uma função de pertinência

triangular eram equações simples de retas, que utilizavam três variáveis fornecidas pelo usuário para serem construídas, apresentadas nas equações 1 e 2.

4

Figura 1 : Erros na função de pertinência triangular

(a)Alterações em ambos os lados do triângulo, convexo - convexo e côncavo – côncavo, (b)Alterações em ambos os lados do triângulo, côncavo - convexo e convexo – côncavo,

(c)Alterações em apenas um lado do triângulo, normal - côncavo e côncavo – normal,(d)Alterações em apenas um lado do triângulo, normal - convexo e convexo –

normal

Figura 2: Exemplo de uma função de pertinência triangular

O novo módulo apresentado neste relatório permite, através das modificações realizadas, que o usuário utilize durante a geração de uma função de pertinência mais duas variáveis. A primeira variável (tipo_erro), determinará o tipo de erro a ser estudado. A segunda variável (erro_per) determina o valor percentual do erro escolhido, que pode variar de 0 a 100%.

5

Os diferentes tipos de erro apresentados na figura 1 podem ser obtidos, agora, da seguinte forma:

Tabela 1: Valores dos parâmetros para os diferentes tipos de erro Tipo de erro Valor do parâmetro nenhum erro 0 (valor padrão)

convexo – convexo 1 côncavo – côncavo 2 côncavo – convexo 3 convexo – côncavo 4 normal – côncavo 5 côncavo – normal 6 normal – convexo 7 convexo – normal 8

Para que estes tipos de erros pudessem ser implementados foram feitas modificações nas equações que criam a função de pertinência triangular. As equações de reta foram substituídas por equações de parábola com índice “n”. Assim, tem-se:

Lado esquerdo (inclinação positiva)

Erro tipo convexo Erro tipo côncavo

( )

( )( )

n

babx

y

babtxyerro

n

typererro

tyyerro

abatx

ty

aab

tx

⎟⎟⎠

⎞⎜⎜⎝

⎛

−

−−=

⎟⎠

⎞⎜⎝

⎛−

−

−=

×⎟⎠

⎞⎜⎝

⎛+=

−

−=

+⎟⎠

⎞⎜⎝

⎛ −=

1

log

_1log100_

_

2

10

10

( )( )

n

abax

y

abatxyerro

n

typererro

tyyerro

abatx

ty

aab

tx

⎟⎟⎠

⎞⎜⎜⎝

⎛

−

−=

⎟⎠

⎞⎜⎝

⎛−

−=

×⎟⎠

⎞⎜⎝

⎛−=

−

−=

+⎟⎠

⎞⎜⎝

⎛ −=

10

10

log

_log100_

_

2

6

Lado direito (inclinação negativa)

Erro tipo convexo Erro tipo côncavo

( )

( )( )

n

bcbx

y

bcbtxyerro

n

typererro

tyyerro

bctxc

ty

bbc

tx

⎟⎟⎠

⎞⎜⎜⎝

⎛

−

−−=

⎟⎠

⎞⎜⎝

⎛−

−

−=

×⎟⎠

⎞⎜⎝

⎛+=

−

−=

+⎟⎠

⎞⎜⎝

⎛ −=

1

log

_1log100_

_

2

10

10

( )( )

n

cbcx

y

cbctxyerro

n

typererro

tyyerro

bctxc

ty

bbc

tx

⎟⎟⎠

⎞⎜⎜⎝

⎛

−

−=

⎟⎠

⎞⎜⎝

⎛−

−=

×⎟⎠

⎞⎜⎝

⎛−=

−

−=

+⎟⎠

⎞⎜⎝

⎛ −=

10

10

log

_log100_

_

2

Assim através dos valores apresentados na tabela 1 consegue-se os diferentes

tipos de erro desejados.

4. Teste do Sistema

Para se efetuar os testes no sistema foi utilizado o controlador difuso descrito na referência [6]. Este controlador possui 2 entradas e somente uma saída, cujas funções de pertinência podem ser visualizadas nas figuras 3, 4 e 5. Para apresentação e simulação do sistema usou-se o “toolbox Fuzzy” do MATLAB.

A base de regras do controlador foi sintetizada na tabela 2, onde “e” representa a variável de entrada erro e “Δe” representa a variável de entrada variação do erro.

Tabela 2: Base de regras do controlador difuso utilizado e\ Δe NH NL ZI PL PH NH NLG NLG NM NS ZO NL NLG NM NS ZO PS ZI NM NS ZO PS PM PL NS ZO PS PM PLG PH ZO PS PM PLG PLG

7

O método de focalização utilizado foi o do centro de gravidade e o mecanismo de inferência é baseado no método de Mandani.

Figura 3:Funções de pertinência da entrada 1 - Erro

Figura 4 :Funções de pertinência da entrada 2 - Variação do Erro

8

Figura 5:Funções de pertinência de saída

Com a finalidade de se testar a resposta deste controlador difuso foi utilizado um

sistema realimentado cuja planta possui o seguinte modelamento:

SSSG

10300)( 2 +

=

O sistema completo pode ser visualizado através da figura a seguir.

Figura 6: Sistema realimentado utilizado durantes os testes do controlador difuso

Como pode ser visto na figura anterior foi utilizado um sinal em forma de degrau para simular a entrada erro e a diferença entre o degrau e a resposta do sistema como variável de entrada variação do erro.

9

O usuário através da interface apresentada na figura 7, no item “params”, coloca os valores apresentados na tabela 1 e o valor percentual do tipo de erro escolhido para gerar a função desejada.

Figura 7: Localização do item "params"

O exemplo a seguir mostra como se obteve uma função triangular, com erro do

tipo 1, e com 30% de erro de linearidade. Para a criação de uma função de pertinência triangular, com erro de linearidade,

altera-se o quarto parâmetro com o tipo de erro que se quer gerar(1 a 8) e no lugar do quinto parâmetro coloca-se o valor percentual deste erro (0 %100%). Quando se cria uma nova função de pertinência, os valores destes dois parâmetros são inseridos automaticamente com valores nulos, devendo-se completar com os parâmetros que definem a função desejada (figura 8).

Após a criação da função de pertinência volta-se a editar o valor do parâmetros

no item “params”. Isto pode ser conseguido apenas clicando na caixa do item “params”. Após a alteração dos valores do quarto e quinto parâmetro para 1 e 30 respectivamente, obtem-se a figura 9.

10

Figura 8: Função de pertinência original - nenhum erro implementado

Figura 9: Função de pertinência original alterada

com 30% de erro do tipo 1 (convexo-convexo) Nos itens 4.1 e 4.2 serão apresentados os resultados obtidos variando-se os tipos

de erros implementados no módulo gerador de erros e respectivos comentários.

11

4.1. Primeira fase de testes

Na primeira fase de testes serão introduzidos erros em todas funções de pertinência triangular presentes no sistema sendo que, cada tipo de erro foi gerado com diferentes valores percentuais (5%, 10%, 20%, 30% e 50%).

Como forma de identificação dos diferentes valores de erros, nesta fase de testes, será utilizada a seguinte convenção de cores:

Tabela 3: Convenção de cores para os gráficos da primeira fase de testes Cor Valor do erro Lilás 0% - valor original sem erro

Azul Claro 5% Vermelho 10%

Verde 20% Azul Escuro 30%

Amarelo 50%

4.1.1. Erro tipo 1 – Convexo-Convexo

Foram introduzidos erros do tipo 1 em todas as funções de pertinência do tipo triangular presentes no controlador difuso testado, variando este erro entre 5 e 50%. A figura seguinte apresenta a resposta do sistema ao degrau unitário, para esta faixa de variação do erro.

Figura 10:Resposta do sistema ao erro tipo 1 - Convexo-Convexo

12

Pode-se notar que este tipo de erro praticamente não altera a resposta do sistema, mesmo com uma diferença de 50% em relação à função de pertinência original.

4.1.2. Erro tipo 2 – Côncavo-Côncavo


Figura 11:Resposta do sistema ao erro

tipo2 - Côncavo-Côncavo

Novamente podemos perceber que este tipo de erro não resultou em grandes alterações na resposta do sistema.

4.1.3. Erro tipo 3 – Côncavo-Convexo


Com a aplicação deste tipo de erro podemos dizer que as alterações de

comportamento são graves e, como era de se esperar, aumentam junto com o valor do erro. Pode-se dizer também que este erro ocasionou um atraso na resposta ao degrau e até mesmo uma instabilidade do sistema.

13

Figura 12:Resposta do sistema ao erro tipo 3 - Côncavo-Convexo

4.1.4. Erro tipo 4 – Convexo-Côncavo


Figura 13Resposta do sistema ao erro tipo 4 - Convexo-Côncavo

14

Aqui a resposta do sistema foi totalmente alterada ocasionando uma instabilidade visível e crescente, conforme o valor do erro é aumentado.

4.1.5. Erro tipo 5 – Normal-Côncavo


Figura 14:Resposta do sistema ao erro tipo 5 - Normal-Côncavo

Este tipo de erro ocasionou o mesmo comportamento que o erro anterior

provocou, mas de uma forma menos pronunciada, pois os erros de 5% e 10% podem chegar a ser aceitáveis por não possuírem um desvio muito alto em relação à resposta original do sistema, o que não ocorria com o erro tipo 4.

4.1.6. Erro tipo 6 – Côncavo-Normal


Da mesma forma que o erro anterior este erro em relação ao erro tipo 3 pode ser,

dependendo da aplicação, aceitável para erros da faixa de 5% e 10%, pois nestas faixas o desvio em relação à resposta original não é muito grande.

15

Figura 15:Resposta do sistema ao erro tipo 6 - Côncavo-Normal

4.1.7. Erro tipo 7 – Normal-Convexo


Figura 16:Resposta do sistema ao erro tipo 7 - Normal-Convexo

16

Esta resposta se assemelha a respostas aos erro tipo 3 e 6, porém esta resposta parece ser mais aceitável do que estes, pois o erros de 5%, 10% e 20% parecem rumar para um valor estável e com reduzido desvio em relação à resposta original.

4.1.8. Erro tipo 8 – Convexo-Normal


Figura 17:Resposta do sistema ao erro tipo 8 - Convexo-Normal

Da mesma forma que o erro tipo 7 apresenta semelhanças com os erros do tipo 3

e 6, este erro possui resposta semelhante ao erros do tipo 4 e 5. Porém, somente os erros da faixa de 5% e 10% parecem confiáveis e com tendência de estabilização.

4.2. Segunda fase de testes

Nesta fase será utilizada como forma de identificação dos diferentes valores de erros, a seguinte convenção de cores:

Tabela 4: Convenção de cores para os gráficos da primeira fase de testes Cor Valor do erro Lilás 0% - valor original sem erro

Azul Claro 0,5% Vermelho 1%

Verde 5%

17

4.2.1. Erro tipo 1 – Convexo-Convexo


Figura 18:Resposta do sistema ao erro tipo 1 - Convexo-Convexo

Com a análise dos dados da simulação foi possível construir a tabela a seguir.

Onde constam, em valores percentuais, o desvio relativo entre a resposta do sistema com um controlador difuso sem erros e a resposta do mesmo sistema com um controlador difuso que possui erros em suas funções de pertinência.

Tabela 5: Desvio relativo percentual ocorrido em virtude de erros do tipo 1

Valor % do erro gerado Desvio no tempo (x) Desvio no valor final (y) 0,5 0 % 0 % 1 0 % 0 % 5 0 % 0 %

Pode-se notar que este tipo de erro não altera a resposta do sistema, ou seja, um

controlador difuso que possua este tipo de erro em suas funções de pertinência continuará a responder perfeitamente às entradas do sistema.

4.2.2. Erro tipo 2 – Côncavo-Côncavo

Foram introduzidos erros do tipo 2 em todas as funções de pertinência do tipo triangular presentes no controlador difuso testado, variando este erro entre 0,5 e 5%. A

18

figura seguinte apresenta a resposta do sistema ao degrau unitário, para esta faixa de variação do erro.

Figura 19:Resposta do sistema ao erro tipo2 - Côncavo-Côncavo




Valor % do erro gerado Desvio no tempo (x) Desvio no valor final (y) 0,5 0 % 0 % 1 0 % 0 % 5 0 % 0 %

Pode-se notar que este tipo de erro também não altera a resposta do sistema, ou

seja, um controlador difuso que possua este tipo de erro em suas funções de pertinência continuará a responder perfeitamente às entradas do sistema.

4.2.3. Erro tipo 3 – Côncavo-Convexo

Foram introduzidos erros do tipo 3 em todas as funções de pertinência do tipo triangular presentes no controlador difuso testado, variando este erro entre 0,5 e 5%. A figura seguinte apresenta a resposta do sistema ao degrau unitário, para esta faixa de variação do erro.

19

Figura 20:Resposta do sistema ao erro tipo 3 - Côncavo-Convexo




Valor % do erro gerado Desvio no tempo (x) Desvio no valor final (y) 0,5 0 % 0,33 % 1 0 % 0,66 % 5 0 % 2,64 %

Com a aplicação deste tipo de erro podemos dizer que as alterações de

comportamento são visíveis e, como era de se esperar, aumentam junto com o valor do erro. Pode-se dizer também que este erro, mesmo possuindo um desvio nulo no tempo de resposta, provocou um atraso na estabilização do sistema.

4.2.4. Erro tipo 4 – Convexo-Côncavo


20

Figura 21Resposta do sistema ao erro tipo 4 - Convexo-Côncavo





Da mesma forma que o erro do tipo 3, a aplicação deste tipo de erro resulta em

visíveis alterações de comportamento que aumentam junto com o valor do erro. Pode-se dizer também que este erro, mesmo possuindo um desvio nulo no tempo de resposta, provocou um atraso na estabilização do sistema.

4.2.5. Erro tipo 5 – Normal-Côncavo


21

Figura 22:Resposta do sistema ao erro tipo 5 - Normal-Côncavo





O comportamento do sistema com este tipo de erro é muito semelhante ao

comportamento do teste anterior (controlador com erro tipo 4). Mas este, diferentemente do anterior, o sistema não apresenta nenhum tipo de atraso na estabilização do sistema. O que torna estes erros perfeitamente aceitáveis em um sistema com um controlador difuso.

4.2.6. Erro tipo 6 – Côncavo-Normal


22

Figura 23:Resposta do sistema ao erro tipo 6 - Côncavo-Normal




Valor % do erro gerado Desvio no tempo (x) Desvio no valor final (y) 0,5 0 % 0 % 1 0 % 0,33 % 5 0 % 1,65 %


comportamento do teste do controlador com erro tipo 3. Mas este, diferentemente do anterior, o sistema não apresenta nenhum tipo de atraso na estabilização do sistema. O que torna estes erros perfeitamente aceitáveis em um sistema com um controlador difuso.

4.2.7. Erro tipo 7 – Normal-Convexo


23

Figura 24:Resposta do sistema ao erro tipo 7 - Normal-Convexo






comportamento do teste do controlador com erros tipo 6. Mas este possui valores desvio no valor final menores que os obtidos no teste anterior. Portanto este tipo de erro, nesta faixa de variação, se torna perfeitamente aceitável em um sistema com um controlador difuso.

4.2.8. Erro tipo 8 – Convexo-Normal


24

Figura 25:Resposta do sistema ao erro tipo 8 - Convexo-Normal






comportamento do teste do controlador com erros tipo 5. Mas este possui valores desvio no valor final menores que os obtidos no teste anterior. Portanto este tipo de erro, nesta faixa de variação, se torna perfeitamente aceitável em um sistema com um controlador difuso.

4.3. Análise geral

Após os testes feitos no itens anteriores pode-se concluir que os tipos de erros que menos afetam a performance do controlador difuso testado são os do tipo 1 e 2.

Estes erros não comprometeram a resposta do sistema mesmo com erros da faixa

de 50%, o que indica que se um sistema que utilize um controlador difuso com estes tipos de erro pode vir a ter seu projeto simplificado sem que este comprometa o processo a ser controlado.

25

Para erros na faixa da segunda fase de testes (0,5 a 5%) os erros do tipo 5, 6, 7 e 8 também não afetam sensivelmente a performance do controlador difuso.

5. Conclusões

Durante todo o período deste projeto de iniciação científica, acredito que os diversos assuntos com os quais eu tive contato foram extremamente importantes para a formação deste bolsista. Posso citar como principais assuntos o projeto de controladores difusos e o conhecimento e conseqüente aprofundamento nas técnicas de programação e utilização da ferramenta MATLAB.

O projeto desenvolvido mostrou que, para pequenos desvios na linearidade da

função de pertinência, como acontece em projetos de circuitos integrados, a resposta do sistema não apresentou erros que inviabilizem o desenvolvimento de microprocessadores integrados com as técnicas utilizadas atualmente.

Com o presente relatório conclui-se todo o cronograma deste projeto de

iniciação científica. Acredito que o módulo gerador de erros deve passar por mais testes com outros tipos de controladores, sistemas e entradas e, finalmente, também ser testado em situações práticas, ou seja, comparar os resultados da simulação com os resultados obtidos por testes em um sistema real que possua um controlador difuso.

________________________ ________________________ Fernando Setra Dantas Galdenoro Botura Jr.

Bolsista Orientador

26

6. Referências Bibliográficas [1] Zadeh, L, Fuzzy Sets, Information and Control, no 8, 338-353, 1965. [2] Zadeh, L, Making computers think like people, IEEE Spectrum, August 1984. [3] Sugeno, M., An Introduction Survey of Fuzzy Control, Information Sciences 36, 59-83, 1985. [4] Zadeh, L., Fuzzy Logic, IEEE, April 1988. [5] Pedrycz, W. and Gomide, F., An Introduction to Fuzzy Sets – Analysis and Design, MIT Press – Cambridge, 1998. [6]Campo, Inés del and Tarela, José Manuel, “Consequences of the Digitization on the Performance of a Fuzzy Logic Controler”, IEEE, February 1999. [7] Timothy A. Adcock, “Digital Signal Processing”, Semiconductor Group, Texas Instruments Incorporated, Janeiro 1993. [8] Klir, G. J., Yuan, B., “Fuzzy Sets and Fuzzy Logic - Theory and Aplications”, Prentice Hall, pp 333-334, 1995 [9] D. Driankov, H. Hellendoorn, M. Reinfrank, “An Introduction to Fuzzy Control”, Springer, 2ªedição, pp134, 1996 [10] “Fuzzy Logic” - http://www.abo.fi/~rfuller/fuzs.html [11] “Fuzzy Logic Sources of Information” - http://www.cms.dmu.ac.uk/~rij/fuzzy.html [12] “Artificial Intelligence Publications” - http://oingo.com/topic/11/11993.html [13] Berkan, Riza C. and Trubatch, Sheldon L., “Fuzzy Systems Design Principles” [14]Schwartz, Daniel G. and Klir, George J., “Fuzzy Logic Flowers i Japan”, IEEE Spectrum, July 1992. [15] Gulley, Ned and Jang,J.S. Roger, “Fuzzy Logic Toolbox for use with MATLAB”

27

ANEXOS

28

function y = trimf(x, params) %TRIMF Triangular membership function. % TRIMF(X, PARAMS) returns a matrix which is the triangular % membership function evaluated at X. PARAMS = [A B C] is a 3-element % vector that determines the break points of this membership function. % Usually we require A <= B <= C. % % Note that this MF always has a height of unity. To have a triangular % MF with a height less than unity, use TRAPMF instead. % % For example: % % x = (0:0.2:10)'; % y1 = trimf(x, [3 4 5]); % y2 = trimf(x, [2 4 7]); % y3 = trimf(x, [1 4 9]); % subplot(211), plot(x, [y1 y2 y3]); % y1 = trimf(x, [2 3 5]); % y2 = trimf(x, [3 4 7]); % y3 = trimf(x, [4 5 9]); % subplot(212), plot(x, [y1 y2 y3]); % set(gcf, 'name', 'trimf', 'numbertitle', 'off'); % % See also DSIGMF, GAUSS2MF, GAUSSMF, GBELLMF, EVALMF, PIMF, PSIGMF, % SIGMF, SMF, TRAPMF, ZMF. % Roger Jang, 6-29-93, 10-5-93, 4-14-94. % Copyright (c) 1994-96 by The MathWorks, Inc. % $Revision: 1.11 $ $Date: 1996/04/02 23:21:40 $ if nargin ~= 2 error('Two arguments are required by the triangular MF.'); elseif length(params) < 5 error('The triangular MF needs at least five parameters.'); end a = params(1); b = params(2); c = params(3); erro = params(4); erro_ind = abs(params(5)); if a > b, error('Illegal parameter condition: a > b'); elseif b > c, error('Illegal parameter condition: b > c'); elseif a > c, error('Illegal parameter condition: a > c'); end if (erro==0) left=0; right=0; elseif (erro==1) left=1; right=1; elseif (erro==2) left=-1; right=-1; elseif (erro==3) left=-1;

29

right=1; elseif (erro==4) left=1; right=-1; elseif (erro==5) left=0; right=-1; elseif (erro==6) left=-1; right=0; elseif (erro==7) left=0; right=1; elseif (erro==8) left=1; right=0; else error('Illegal parameter'); end y = zeros(size(x)); % Left and right shoulders (y = 0) index = find(x <= a | c <= x); y(index) = zeros(size(index)); % Left slope if (a ~= b) index = find(a < x & x < b); tx = ((b-a)/2)+a; ty = (tx-a)/(b-a); if (left==0) y(index) = (x(index)-a)/(b-a); elseif (left==-1) erro_y = ty-(erro_ind/100)*ty; tz = (tx-a)/(b-a); n = log10(erro_y)/log10(tz); z(index) = (x(index)-a)/(b-a); y(index) = z(index).^n; elseif (left==1) erro_y = (ty-(-erro_ind/100)*ty); tz =(tx-b)/(a-b); n = log10(1-erro_y)/log10(tz); z(index) =(x(index)-b)/(a-b); y(index) = 1-z(index).^n; else

30

error('Illegal parameter'); end end % right slope if (b ~= c) index = find(b < x & x < c); tx = ((c-b)/2)+b; ty = (c-tx)/(c-b); if (right==0) y(index) = (c-x(index))/(c-b); elseif (right==1) erro_y = ty-(-erro_ind/100)*ty; tz = (tx-b)/(c-b); n = log10(1-erro_y)/log10(tz); z(index) =(x(index)-b)/(c-b); y(index) =1-z(index).^n; elseif (right==-1) erro_y = ty-(erro_ind/100)*ty; tz = (tx-c)/(b-c); n = log10(erro_y)/log10(tz); z(index) =(x(index)-c)/(b-c); y(index) = z(index).^n; else error('Illegal parameter'); end end % Center (y = 1) index = find(x == b); y(index) = ones(size(index));

31

%close all; clear all; a=readfis('normal'); b=readfis('erro'); [x1 y1 z1]=gensurf(a); [x2 y2 z2]=gensurf(b); x3=x1; y3=y1; z3=100.*(z1-z2); x4=x1; y4=y1; z4=100.*((z1-z2)./z1); figure(6) surf(x1,y1,z1) xlabel('entrada 1'); ylabel('entrada 2'); zlabel('saída'); title('Superfície Original'); figure(7) surf(x2,y2,z2) xlabel('entrada 1'); ylabel('entrada 2'); zlabel('saída'); title('Superfície com Erro'); figure(8) surf(x3,y3,z3) xlabel('entrada 1'); ylabel('entrada 2'); zlabel('erro em %'); title('Erro absoluto %'); rotate3d on; figure(9) surf(x4,y4,z4) xlabel('entrada 1'); ylabel('entrada 2'); zlabel('erro em %'); title('Erro relativo %'); rotate3d on; figure(10) set(10,'Name',['Valores Máximos e Mínimos'], ... 'NumberTitle','off', ... 'MenuBar','none',... 'Color',[1 1 1],... 'Position',[0 0 300 300]) axis off; hold on; x=0; y=100; color=[0 0 0]; fill([ 0 0 30 30],[ 0 100 100 0],'w')

32

text(x+8,y-8,{'Valor Máximo'},'Color',color); text(x+20,y-8,{'Valor Mínimo'},'Color',color); text(x+1,y-30,{'Erro ';'absoluto %';'Erro ';'relativo %'},'Color',color); text(x+11,y-24,{num2str(max(max(z3)),'%6.2f %')},'Color',color); text(x+22,y-24,{num2str(min(min(z3)),'%6.2f %')},'Color',color); text(x+11,y-36,{num2str(max(max(z4)),'%6.2f %')},'Color',color); text(x+22,y-36,{num2str(min(min(z4)),'%6.2f %')},'Color',color);

Universidade Estadual Paulista - Unesp · SE A acontecer e B ocorrer, ENTÃO faça-se C...

Documents

Transcript of Universidade Estadual Paulista - Unesp · SE A acontecer e B ocorrer, ENTÃO faça-se C...