20/09/201120/09/2011 11

VALIDAVALIDAÇÇÃO DE UM MODELO DE ÃO DE UM MODELO DE POTENCIAIS ESCALARES COM POTENCIAIS ESCALARES COM

CONTORNO RUGOSOS PELO MCONTORNO RUGOSOS PELO MÉÉTODO TODO DOS ELEMENTOS FINITOSDOS ELEMENTOS FINITOS

Proposta de Tese de Doutorado deProposta de Tese de Doutorado de

Lucas MLucas Mááximo Alvesximo AlvesDOUTORANDODOUTORANDO

Luiz Luiz AlkiminAlkimin de Lacerdade LacerdaORIENTADORORIENTADOR

JosJoséé de Antonio Marques de Antonio Marques CarrerCarrerCOCO--ORIENTADORORIENTADOR

20/09/201120/09/2011 22

ÍÍndicendice INTRODUINTRODUÇÇÃO ÃO -- ConsideraConsideraçções Iniciaisões Iniciais PROPOSIPROPOSIÇÇÃO DO PROBLEMAÃO DO PROBLEMA INTRODUINTRODUÇÇÃO A TEORIA FRACTAL DE MEDIDAÃO A TEORIA FRACTAL DE MEDIDA FUNDAMENTAFUNDAMENTAÇÇÃO TEÃO TEÓÓRICARICA O Problema do Potencial com Contorno Regular O Problema do Potencial com Contorno Regular

(Euclidiano ou Liso) (Euclidiano ou Liso) –– P1P1 O Problema do Potencial com Contorno Irregular O Problema do Potencial com Contorno Irregular

(Fractal ou Rugoso) (Fractal ou Rugoso) –– P2P2 ModelamentoModelamento Fractal do Problema Equivalente Fractal do Problema Equivalente -- PEPE MATERIAIS E MMATERIAIS E MÉÉTODOSTODOS RESULTADOSRESULTADOS DISCUSSÃO.DISCUSSÃO. CONCLUSÕESCONCLUSÕES

20/09/201120/09/2011 33

INTRODUINTRODUÇÇÃO ÃO -- ConsideraConsideraçções iniciaisões iniciaisEste trabalho foi motivado pelas seguintes Este trabalho foi motivado pelas seguintes

circunstâncias cientcircunstâncias cientííficas e tecnolficas e tecnolóógicas:gicas:

A Geometria Fractal descreve Estruturas IrregularesA Geometria Fractal descreve Estruturas Irregulares Novas Propostas de Modelagem de Estruturas Irregulares Novas Propostas de Modelagem de Estruturas Irregulares

usando a Teoria Fractal (Literatura Especializada)usando a Teoria Fractal (Literatura Especializada) Revisão de Modelos ClRevisão de Modelos Cláássicos que têm como base a ssicos que têm como base a

Geometria Euclidiana (Literatura Especializada)Geometria Euclidiana (Literatura Especializada) A Mecânicas (do ContA Mecânicas (do Contíínuo, Calor, Fluidos, Snuo, Calor, Fluidos, Sóólidos, lidos,

Fratura), não leva em conta o Efeito da Rugosidade na sua Fratura), não leva em conta o Efeito da Rugosidade na sua DescriDescriçção Matemão Matemáática.tica.

Entender o Processo de DissipaEntender o Processo de Dissipaçção de Energia nos ão de Energia nos Fenômenos que Apresentam GeomFenômenos que Apresentam Geoméétricas Irregularestricas Irregulares

20/09/201120/09/2011 44

Objetivos do TrabalhoObjetivos do Trabalho i) Descrever Anali) Descrever Analíítica e Numericamente o Fenômenos tica e Numericamente o Fenômenos

FFíísicos utilizandosicos utilizando--se Mse Méétodos Numtodos Numééricos e a Geometria ricos e a Geometria Fractal.Fractal.

ii) Validar Modelos de Rugosidade Fractal utilizando ii) Validar Modelos de Rugosidade Fractal utilizando MMéétodo Numtodo Numééricos Aplicado a um Problema de Potencial ricos Aplicado a um Problema de Potencial Escalar. Escalar. Por exemplo, Transmissão de Calor em Por exemplo, Transmissão de Calor em Corpos que apresentam uma Geometria Irregular Corpos que apresentam uma Geometria Irregular Bordas Rugosas.Bordas Rugosas.

iii) Desenvolver um Miii) Desenvolver um Méétodo Numtodo Numéérico de Crico de Cáálculo a ser lculo a ser Implantado em um Software BImplantado em um Software Báásico de Simulasico de Simulaçção de ão de Fenômenos com Rugosidade.Fenômenos com Rugosidade.

iv) Validar Resultados Teiv) Validar Resultados Teóóricos dos Modelos Propostos ricos dos Modelos Propostos atravatravéés de Ensaios e Testes Conclusivos. s de Ensaios e Testes Conclusivos.

v) Propor correv) Propor correçções ou Novos Modelos de ões ou Novos Modelos de FenomenolFenomenolóógicos com a Descrigicos com a Descriçção Analão Analíítica da tica da Rugosidade. Rugosidade.

20/09/201120/09/2011 55

INTRODUINTRODUÇÇÃO A TEORIA FRACTAL DE ÃO A TEORIA FRACTAL DE MEDIDAMEDIDA

FRACTAISFRACTAIS:: são objetos geomsão objetos geoméétricos autotricos auto--invariantes por transformainvariantes por transformaçção de escala ão de escala que que possuem possuem dimensão fraciondimensão fracionáária ria

Invariância por TransformaInvariância por Transformaçção de Escalaão de Escala -- (partes (partes semelhantes ao todo). semelhantes ao todo). = = lloo//LLoo (fator de escala)(fator de escala) que pode que pode ser por:ser por:

AUTOAUTO--SIMILARIDADESIMILARIDADE ou ou AUTOAUTO--AFINIDADEAFINIDADE..(Ex. um Pinheiro) (Ex. uma Trinca)(Ex. um Pinheiro) (Ex. uma Trinca)

A Extensão do ObjetoA Extensão do Objeto, , MMdd, , depende do tamanho da depende do tamanho da rréégua de medida utilizada, gua de medida utilizada, LLoo, isto , isto éé,,

MMdd(() = ) = MMdododd--D D se se D = d D = d MMdd(() = ) = MMdodo..

20/09/201120/09/2011 66

Invariância por TransformaInvariância por Transformaçção de ão de EscalaEscala

Def: Partes Semelhantes Def: Partes Semelhantes ao Todoao Todo

Exemplo: Exemplo: PinusPinus

Outros Exemplos:Outros Exemplos:Nuvens, Trincas, Cristais Nuvens, Trincas, Cristais

de Gelo, Rochas,de Gelo, Rochas,Rios, Cidades, Rios, Cidades, etcetc((NiveisNiveis HierHieráárquicos de rquicos de

Estruturas)Estruturas)

20/09/201120/09/2011 77

Para que servem na PrPara que servem na Práática?tica? Servem para se Descrever Matematicamente Servem para se Descrever Matematicamente

Estruturas Irregulares, que a Geometria Euclidiana dos Estruturas Irregulares, que a Geometria Euclidiana dos Elementos BElementos Báásicos: Ponto, Reta, Plano e Espasicos: Ponto, Reta, Plano e Espaçço não o não éécapazcapaz

Geometria Irregular Geometria IrregularGeometria Irregular Geometria Irregular

Modelagem GeomModelagem Geoméétricatrica

20/09/201120/09/2011 88

AutoAuto--SimilaridadeSimilaridade Fractal autoFractal auto-- similar similar Dx = Dx = DyDy = = Dz = D;Dz = D;

d d Di Di d+1 ; d+1 ; Dx + Dx + DyDy + Dz = d+1+ Dz = d+1d = dimensão de projed = dimensão de projeçção ; d+ 1 = dimensão de imersãoão ; d+ 1 = dimensão de imersão

20/09/201120/09/2011 99

AutoAuto--AfinidadeAfinidade Fractal AutoFractal Auto-- Afim: Uma Afim: Uma

Dimensão Fractal Dimensão Fractal Diferente para cada Diferente para cada DireDireççãoão

Dx = Dx = DyDy HHd d D D d+1d+1

Dx + Dx + DyDy + H = d+1+ H = d+1

d = dimensão de projed = dimensão de projeççãoão

d+ 1 = dimensão de imersãod+ 1 = dimensão de imersão

20/09/201120/09/2011 1010

Exemplos de Fractais:Exemplos de Fractais: Geom.Euclidiana x FractalGeom.Euclidiana x Fractal Fractais MatemFractais Matemááticos e ticos e

FFíísicos ou Naturaissicos ou Naturais

20/09/201120/09/2011 1111

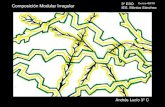
Modelagem Fractal de uma Cadeia Modelagem Fractal de uma Cadeia de Montanhasde Montanhas

FunFunçções Exatas ou Funões Exatas ou Funçções Aproximadasões Aproximadas

20/09/201120/09/2011 1212

Antecedentes HistAntecedentes Históóricosricos Uma modificaUma modificaçção da Mecânica da Fratura foi proposta mas ão da Mecânica da Fratura foi proposta mas

alguns resultados ainda precisam ser validados alguns resultados ainda precisam ser validados corretamentecorretamente

ALVES, Lucas MALVES, Lucas Mááximo Rosana Vilarim da Silva, ximo Rosana Vilarim da Silva, Bernhard Joachim Mokross, Bernhard Joachim Mokross, TheThe influenceinfluence ofof thethe crackcrackfractal fractal geometrygeometry onon thethe elasticelastic plasticplastic fracturefracturemechanicsmechanics. . PhysicaPhysica A: Statistical Mechanics and its A: Statistical Mechanics and its ApplicationsApplications. Vol. 295, n. 1/2, p. 144. Vol. 295, n. 1/2, p. 144--148, 12 June 2001.148, 12 June 2001.

ALVES, Lucas MALVES, Lucas Mááximo: Fractal geometry concerned ximo: Fractal geometry concerned with stable and dynamic fracture mechanics. with stable and dynamic fracture mechanics. Journal of Journal of TheorethicalTheorethical and Applied Fracture Mechanicsand Applied Fracture Mechanics, , VolVol 44/1, 44/1, pp 44pp 44--57, 2005.57, 2005.

20/09/201120/09/2011 1313

MECÂNICA DA FRATURAMECÂNICA DA FRATURA

ModeloModelo de de umauma placaplacaplanaplana e e infinitainfinita de de espessuraespessura desprezdesprezíívelvelsujeitasujeita a a umauma tensãotensãoremotaremota, , = cte= cte..

EstaEsta teoriateoria nãonão levaleva em em contaconta a a rugosidaderugosidade das das superfsuperfííciescies de de fraturafratura. Por . Por estaesta razãorazão nãonão explicaexplicadiversosdiversos efeitosefeitosdependentesdependentes dadarugosidaderugosidade

20/09/201120/09/2011 1414

Modelagem de SuperfModelagem de Superfíícies Rugosascies Rugosas

SuperfSuperfíícies de cies de FraturaFratura

NNííveis Hierveis Hieráárquicos rquicos de Estruturas para de Estruturas para Modelagem Modelagem TTééoricaorica

20/09/201120/09/2011 1515

Postulados de transformaPostulados de transformaçção da MFão da MF--ClCláássica para a MFssica para a MF--FractalFractal

Equivalência energEquivalência energéética de Irwintica de Irwin

oUUdeformaçãodeEnergia

Invariância das equaInvariância das equaçções para o caminho rugosoões para o caminho rugoso

oUU

superfíciedeEnergia

o

effo

o

oceffc

GLL

GLL 22

20/09/201120/09/2011 1616

O MODELAMENTO FRACTAL DA O MODELAMENTO FRACTAL DA FRATURA ESTFRATURA ESTÁÁVELVEL

BalanBalançço energo energéético de Griffithtico de Griffith--Irwin (Irwin (dF dF –– dUdU dUdU CondiCondiçção de grampos fixos (ão de grampos fixos (dF = dF = XduXdu= 0= 0)) CondiCondiçção Quaseão Quase--EstEstáática de Propagatica de Propagaçção ou Critão ou Critéério rio

de Griffithde Griffith--Irwin (Irwin (JJoo RRoo))

MFMF--ClCláássicassica

MFMF--FractalFractal

o

oo

o

ooo dL

dUR

dLUFdJ

;)(

oeff

oo

oo

oo

dLdL

dLdLRR

dLdL

dLdU

RdLdL

dLUFdJ

2

;)(

0

20/09/201120/09/2011 1717

SimulaSimulaççãoão dada FraturaFratura RugosaRugosa emem MateriaisMateriais

Simulação de uma fratura em um meio frágil com concentradores de tensão distribuido aleatóriamente sobre

o material

20/09/201120/09/2011 1818

MMéétodo Grtodo Grááfico de Medida de fico de Medida de uma Linha ou Superfuma Linha ou Superfíície cie

RugosaRugosa

20/09/201120/09/2011 1919

20/09/201120/09/2011 2020

Modelos de SuperfModelos de Superfíícies de Fraturacies de Fratura

H

o

oo l

LLL 22}(1

= Lo/lo

H

o

o

H

o

o

o

lL

lLH

dLdL

22

22

)(1

))(2(1

20/09/201120/09/2011 2121

O MODELAMENTO FRACTAL DA O MODELAMENTO FRACTAL DA SUPERFSUPERFÍÍCIE DE FRATURACIE DE FRATURA

SuperfSuperfíície ou perfil de cie ou perfil de fratura (fratura (triaxialidadetriaxialidade, , xx, , yy, , zz, ou deforma, ou deformaçção plana, ão plana,

KKICIC = = ctecte))

12

22

12

)2(1

H

o

o

H

o

o

o

Ll

LlH

dLdL

Modelo matemModelo matemáático autotico auto--afim (afim (Dx = Dx = DyDy HH))

22

12

H

o

oo

LlLL

20/09/201120/09/2011 2222

Levantamento de Perfis de Fratura em Levantamento de Perfis de Fratura em CimentoCimento

Perfil de fratura levantado a partir da imagem da superfície de fratura da argamassa de cimento

20/09/201120/09/2011 2323

Modelo Fractal do Comprimento Modelo Fractal do Comprimento RugosoRugoso

Ajuste dos Resultados Ajuste dos Resultados Experimentais com o Experimentais com o Modelo FractalModelo Fractal

Trinca em CimentoTrinca em Cimento0 500 1000 1500 2000 2500 3000 3500

0

1000

2000

3000

4000

5000

6000

Data: Data1_BModel: Self-afine Lucas com HoChi^2 = 5397.90527a 0.67427 ±311.22001Ho 4.555 ±1706.52065H 0.18569 ±0.12576

L

Com

prim

ento

rugo

so L

(pix

els)

Comprimento projetado Lo (pixels)

0 500 1000 1500 2000 2500 3000 35000

1000

2000

3000

4000

5000

6000

Data: Data1_BModel: Self-afine Lucas com HoChi^2 = 3559.72309a 1.77038 ±2871.48876Ho 5.36687 ±7921.55055H 0.08547 ±0.22948

L

Com

prim

ento

rugo

so L

(pix

els)

Comprimento projetado Lo (pixels)

20/09/201120/09/2011 2424

Levantamento de Perfis de Fratura em ArgilaLevantamento de Perfis de Fratura em Argila

Perfil de fratura levantado a partir da imagem da superfície de fratura da argila vermelha

20/09/201120/09/2011 2525

0 200 400 600 800 1000 1200 14000

1000

2000

3000

4000

5000

Data: Data1_BModel: Self-afine Lucas com HoChi^2 = 9119.67022a 0.11897 ±46.98883Ho 7.78943 ±2039.48912H 0.33511 ±0.04644

L

Com

prim

ento

rugo

so L

(pix

els)

Comprimento Projetado Lo (pixels)

Modelo Fractal do Comprimento Modelo Fractal do Comprimento RugosoRugoso

Ajuste dos Resultados Ajuste dos Resultados Experimentais com o Experimentais com o Modelo FractalModelo Fractal

Trinca em CerâmicaTrinca em CerâmicaVermelhaVermelha

0 200 400 600 800 1000 1200 1400 16000

1000

2000

3000

4000

5000

Data: Data1_BModel: Self-afine Lucas com HoChi^2 = 12670.99992a 0.45482 ±1376.97283Ho 3.2094 ±8661.56972H 0.10448 ±0.20991

L

Com

prim

ento

rugo

so L

(pix

els)

Comprimento projetado Lo (pixels)

20/09/201120/09/2011 2626

Problema Euclidiano Problema Euclidiano –– P1P1

( , )o o o ou u x y

( , )o o o o ou u x y

2 ( , ) 0o o o ou x y

EquaEquaçções ões BBáásicassicas

20/09/201120/09/2011 2727

DefiniDefiniçção de Fluxo ão de Fluxo -->>

Lei de Fourier Lei de Fourier -->>

oX

o

d dXJdA dt

o oX XJ k

. 0o

o XXk

t

. 0o

o XXJ

t

O Fluxo Generalizado e as O Fluxo Generalizado e as EquaEquaçções de Campo para ões de Campo para

Geometrias RegularesGeometrias Regulares

20/09/201120/09/2011 2828

Problema NãoProblema Não--Euclidiano Euclidiano –– P2P2

EquaEquaççõesõesBBáásicassicas

( , )u u x y

( , )u u x y

2 ( , ) 0u x y

20/09/201120/09/2011 2929

O Fluxo Generalizado e as O Fluxo Generalizado e as EquaEquaçções de Campo para ões de Campo para

Geometrias IrregularesGeometrias Irregulares

Xo

d dXJdA dt

X XJ k

. 0XXk

t

. 0XXJ

t

DefiniDefiniçção de Fluxo ão de Fluxo -->>

Lei de Fourier Lei de Fourier -->>

20/09/201120/09/2011 3030

Problema Equivalente Problema Equivalente -- PEPE FormulaFormulaçção do Problema ão do Problema

( , )o o ou f u x y

( , )u g u x y

2 2( , ) ( , )o o ou x y h u x y ˆ ˆ2 cos .o oo

du du u r ndn du

2P PE1. ( , , , , , )o o oPE P f u u x y x y

Potencial EscalarPotencial Escalar

Fluxo do EscalarFluxo do Escalar

FunFunçção Distribuião Distribuiçção ão do Escalardo Escalar

EquaEquaçção Proposta ão Proposta para o Fluxo do para o Fluxo do

EscalarEscalar

20/09/201120/09/2011 3131

ComparaComparaçção entre os Problemas ão entre os Problemas P1 x P2P1 x P2

P1P1-- Contorno Contorno Euclidiano Liso Euclidiano Liso ou Regularou Regular

P2 P2 -- Contorno Contorno NãoNão--Euclidiano Euclidiano Fractal ou RegularFractal ou Regular

OBS: OBS: ÉÉ preciso modelar todos os cossenos flutuantes por preciso modelar todos os cossenos flutuantes por meio de algum tipo de correlameio de algum tipo de correlaçção ão –– A Geometria Fractal A Geometria Fractal éé uma delas!uma delas!

20/09/201120/09/2011 3232

Modelagem da RugosidadeModelagem da Rugosidade

Modelagem pelo MModelagem pelo Méétodo dos Cossenos Flutuantestodo dos Cossenos Flutuantes

20/09/201120/09/2011 3333

TTéécnica de cnica de RenormalizaRenormalizaççãoão

RenormalizaRenormalizaççãoão dos dos Cossenos FlutuantesCossenos Flutuantes

:= ( )y ( )cos

:= ( )y ( )cos

( )ln ( )cos ( )ln ( )cos

Cosseno Correlator

-1,5

-1

-0,5

0

0,5

1

1,5

-8 -6 -4 -2 0 2 4 6 8

Angulo (teta)

Cos

(tet

a), c

os(t

eta*

)^(a

lfa_r

)

f(teta)=cos(teta) y(teta)=cos(beta)^(alfa)

cosi i ig

20/09/201120/09/2011 3434

AnAnáálise das Projelise das Projeçções do Contorno ões do Contorno RugosoRugoso

ProjeProjeçção do vetor ão do vetor rr na direna direçção da normal não da normal n

cosˆ.

rnr

dndr j

j

20/09/201120/09/2011 3535

MMéétodo dos Elementos Finitostodo dos Elementos Finitos

Parâmetros Parâmetros e Varie Variááveis veis utilizadas utilizadas no Cno Cáálculolculo

20/09/201120/09/2011 3636

AplicaAplicaçção no Contorno Rugosoão no Contorno Rugoso UtilizaUtilizaçção dos Pontos de Gauss prão dos Pontos de Gauss próóximos ao Contornoximos ao Contorno

20/09/201120/09/2011 3737

RESULTADOS e DISCUSSÃORESULTADOS e DISCUSSÃO

Amplitude do Contorno Rugoso UtilizadoAmplitude do Contorno Rugoso Utilizado

Amplitude Y

8,95

9

9,05

9,1

9,15

9,2

9,25

9,3

9,35

9,4

9,45

0 1 2 3 4 5 6 7 8 9 10

coordenada X

coor

dena

da Y

Y

20/09/201120/09/2011 3838

ComparaComparaçção do Modelo PE x P2 ão do Modelo PE x P2 Resultado da primeira aproximaResultado da primeira aproximaçção feitaão feita

Relação P2 x PEquivalente

0,00E+00

5,00E+01

1,00E+02

1,50E+02

2,00E+02

2,50E+02

0 1 2 3 4 5 6 7 8 9 10coordenada X

Flux

o de

Cal

or

J=Jodu/duo (P2 - Rugoso) J (P2 - Rugoso) Jo (P1 - Euclidiano) J=Jodelta_u/uo*dr/dro (PE-Equivalente)

20/09/201120/09/2011 3939

AnAnáálise do Erro Relativolise do Erro Relativo

Observe: 1Observe: 1-- Erro Relativo ~ FunErro Relativo ~ Funçção Desejadaão DesejadaErro Relativo

-6,00E-01

-4,00E-01

-2,00E-01

0,00E+00

2,00E-01

4,00E-01

6,00E-01

8,00E-01

0 1 2 3 4 5 6 7 8 9 10

coordenada X

Erro

Rel

ativ

o (%

)

Erro Relativo

1-Erro Relativo

0,00E+00

2,00E-01

4,00E-01

6,00E-01

8,00E-01

1,00E+00

1,20E+00

1,40E+00

1,60E+00

0 1 2 3 4 5 6 7 8 9 10coordenada X

1- E

rro R

elat

ivo

(%)

Erro Relativo

20/09/201120/09/2011 4040

ReutilizaReutilizaçção da Informaão da Informaçção do Erro ão do Erro RelativoRelativo

Novo CNovo Cáálculo utilizando o Erro Anterior lculo utilizando o Erro Anterior novamente na Equanovamente na Equaçção de Correão de Correççãoão

Relação P2 x PEquivalente

0,00E+00

5,00E+01

1,00E+02

1,50E+02

2,00E+02

2,50E+02

0 1 2 3 4 5 6 7 8 9 10coordenada X

Flux

o de

Cal

or

J=Jodu/duo (P2 - Rugoso) J (P2 - Rugoso) Jo (P1 - Euclidiano) J=Jodelta_u/uo*dr/dro (PE-Equivalente)

20/09/201120/09/2011 4141

O Erro Relativo MO Erro Relativo Méédio agora diminui e se dio agora diminui e se afasta da Funafasta da Funçção Desejadaão Desejada

Erro Relativo

-4,00E-01

-2,00E-01

0,00E+00

2,00E-01

4,00E-01

6,00E-01

8,00E-01

0 1 2 3 4 5 6 7 8 9 10

coordenada X

Erro

Rel

ativ

o (%

)

Erro Relativo

Nova AnNova Anáálise do Erro Relativolise do Erro Relativo

20/09/201120/09/2011 4242

AnAnáálise de Correlalise de Correlaçção Entre as ão Entre as FunFunçções Real e Aproximadaões Real e Aproximada

Resultado do Problema P2 X Resultado do Resultado do Problema P2 X Resultado do Problema Equivalente Problema Equivalente

y = 0,0043x + 0,4164R2 = 0,7953

0,00E+00

2,00E-01

4,00E-01

6,00E-01

8,00E-01

1,00E+00

1,20E+00

1,40E+00

1,60E+00

1,80E+00

0,00E+00 5,00E+01 1,00E+02 1,50E+02 2,00E+02 2,50E+02

J x J_RetaLinear (J x J_)

20/09/201120/09/2011 4343

CONCLUSÕESCONCLUSÕES

Os Resultados obtidos são promissoresOs Resultados obtidos são promissores Se o Problema Se o Problema –– P2 pode ser resolvido P2 pode ser resolvido

computacionalmente por que utilizar o Problema computacionalmente por que utilizar o Problema Equivalente Equivalente –– PE ?PE ?

-- Reduzir o Custo ComputacionalReduzir o Custo Computacional VerificaVerificaçção de Fenômenos Superficiais e Volumão de Fenômenos Superficiais e Voluméétricos tricos

que anteriormente não poderiam ser observados que anteriormente não poderiam ser observados analiticamente.analiticamente.

SeparaSeparaçção do Problema Fão do Problema Fíísico do Geomsico do Geoméétricotrico NecessitaNecessita--se Anse Anáálise da lise da AcuracidadeAcuracidade da Resposta do da Resposta do

MMéétodo dos Elementos Finitos para o Problema P2 no todo dos Elementos Finitos para o Problema P2 no ContornoContorno

AnAnáálise para Diferentes Rugosidadeslise para Diferentes Rugosidades AnAnáálise Variando alguns parâmetros de controlelise Variando alguns parâmetros de controle

20/09/201120/09/2011 4444

Proposta de Trabalhos Futuros Proposta de Trabalhos Futuros

AnAnáálise Ellise Eláástica Linear (Potencial Vetorial)stica Linear (Potencial Vetorial) AnAnáálise lise ElastoElasto--PlPláásticastica (Potencial Tensorial)(Potencial Tensorial) AnAnáálise da Mecânica da Fratura:lise da Mecânica da Fratura:

-- Processo de Fratura EstProcesso de Fratura Estáável ou Quasevel ou Quase--EstEstáático tico –– Linear e NãoLinear e Não--LinearLinear-- Processo de Fratura InstProcesso de Fratura Instáável ou Dinâmicovel ou Dinâmico--NãoNão--LinearLinear

20/09/201120/09/2011 4545

ReferênciasReferências ALLEN, Martin; Gareth J. Brown; Nick J. Miles, ALLEN, Martin; Gareth J. Brown; Nick J. Miles, -- ””Measurements of Measurements of

boundary fractal dimensionsboundary fractal dimensions””: : review of current techniquesreview of current techniques. . Powder Powder TechnologyTechnology, vol. 84, p.1, vol. 84, p.1--14, 1995. 14, 1995.

BARABBARABÁÁSI, Albert SI, Albert –– LLáászlszlóó; H. Eugene Stanley, Fractal concepts in ; H. Eugene Stanley, Fractal concepts in surface growth, Cambridge University Press, 1995.surface growth, Cambridge University Press, 1995.

BUNDE, Armin; Shlomo Havlin, Fractals in Science, SpringerBUNDE, Armin; Shlomo Havlin, Fractals in Science, Springer--Verlag 1994.Verlag 1994. MANDELBROT, Benoit B, MANDELBROT, Benoit B, Fractal: form chance and dimensionFractal: form chance and dimension, Freeman, , Freeman,

San Francisco, 1977.San Francisco, 1977. MANDELBROT, Benoit B., MANDELBROT, Benoit B., The Fractal Geometry of NatureThe Fractal Geometry of Nature, Freeman, San , Freeman, San

Francisco Francisco -- New York 1982.New York 1982. MANDELBROT, Benoit B.; MANDELBROT, Benoit B.; DannDann E. E. PassojaPassoja & Alvin J. & Alvin J. PaullayPaullay, Fractal , Fractal

character of fracture surfaces of metals, character of fracture surfaces of metals, NaturNature e (London)(London), vol. 308 [5961], , vol. 308 [5961], p. 721p. 721--722, 19 April, 1984.722, 19 April, 1984.

MANDELBROT, B. B., in: MANDELBROT, B. B., in: Dynamics of Fractal SurfacesDynamics of Fractal Surfaces, Edited by Family, , Edited by Family, FereydoonFereydoon. and . and VicsVicséékk, , TamTamááss, World Scientific, Singapore, p. 19, World Scientific, Singapore, p. 19--39. 39. 1991.1991.

RICHARDSON, L. F. The problem of contiguity: an appendix to statRICHARDSON, L. F. The problem of contiguity: an appendix to statistics of istics of deadly quarrels. General Systems Yearbook, n.6, p. 139deadly quarrels. General Systems Yearbook, n.6, p. 139--187, 1961.187, 1961.

VICSVICSÉÉK, K, TamTamááss, , Fractal Growth Fractal Growth PhenonmenaPhenonmena, World Scientific, , World Scientific, Singapore, 1992. Singapore, 1992.